Which Fraction Is Equivalent To 2 5
Treneri
May 13, 2025 · 5 min read
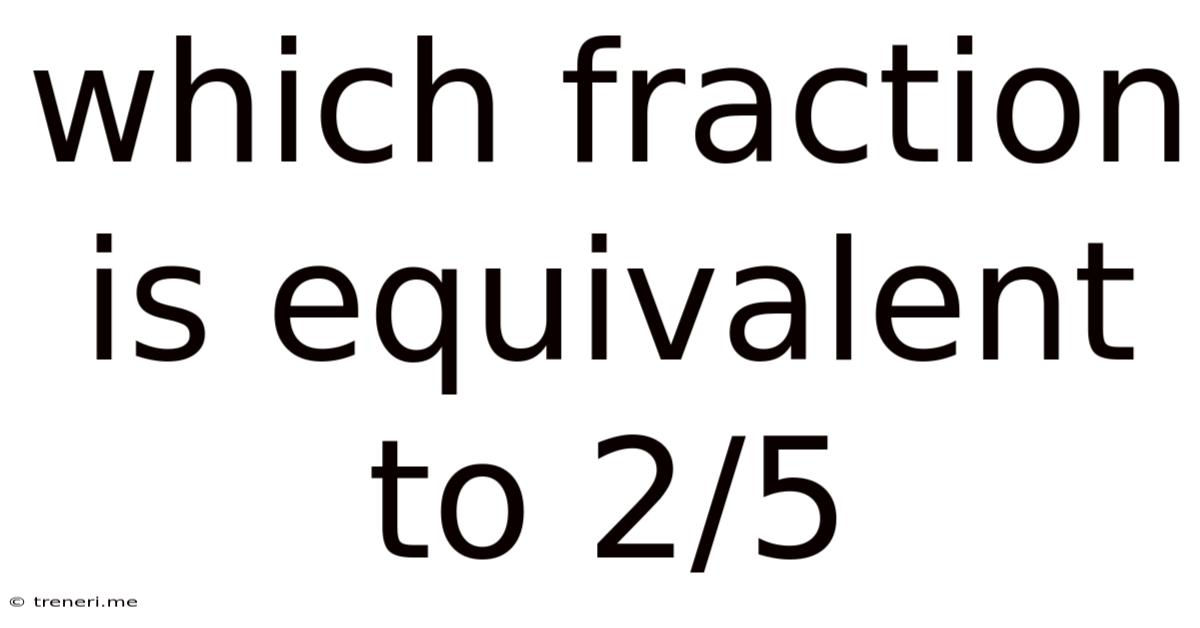
Table of Contents
Which Fraction is Equivalent to 2/5? Understanding Equivalent Fractions and Their Applications
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding various mathematical operations and real-world applications. This comprehensive guide delves into the question: Which fraction is equivalent to 2/5? We'll explore the meaning of equivalent fractions, methods for finding them, and demonstrate their practical uses with numerous examples.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion or value, even though they appear different. They are essentially different ways of expressing the same ratio. Consider a pizza cut into five slices. Two slices represent 2/5 of the pizza. Now, imagine cutting the same pizza into ten slices. Four slices would still represent the same amount, or 4/10 of the pizza. Therefore, 2/5 and 4/10 are equivalent fractions.
The key to understanding equivalent fractions lies in the relationship between the numerator (the top number) and the denominator (the bottom number). To create an equivalent fraction, you multiply or divide both the numerator and the denominator by the same non-zero number. This ensures that the ratio remains unchanged.
Visualizing Equivalent Fractions
Imagine a rectangle divided into five equal parts. If two parts are shaded, it represents 2/5. Now, divide each of the five parts in half. You now have ten parts, and four are shaded. This visually demonstrates that 2/5 is equivalent to 4/10.
!
Methods for Finding Equivalent Fractions
There are several ways to determine equivalent fractions:
1. Multiplying the Numerator and Denominator by the Same Number
This is the most common method. To find an equivalent fraction of 2/5, choose any non-zero whole number (let's say 2) and multiply both the numerator and the denominator by this number:
(2 x 2) / (5 x 2) = 4/10
Similarly, multiplying by 3 gives:
(2 x 3) / (5 x 3) = 6/15
And multiplying by 4 gives:
(2 x 4) / (5 x 4) = 8/20
You can continue this process indefinitely, generating an infinite number of equivalent fractions. All these fractions (4/10, 6/15, 8/20, etc.) represent the same value as 2/5.
2. Dividing the Numerator and Denominator by the Same Number (Simplifying Fractions)
This method is used to simplify fractions to their lowest terms. While the question asks for equivalent fractions, understanding simplification is vital for identifying equivalent fractions. If you were given a fraction like 10/25, you would divide both the numerator and the denominator by their greatest common divisor (GCD), which is 5 in this case:
10 ÷ 5 / 25 ÷ 5 = 2/5
This shows that 10/25 is equivalent to 2/5. Simplifying fractions ensures the fraction is expressed in its most concise form.
3. Using Cross-Multiplication to Check for Equivalence
This method helps verify if two fractions are equivalent. If you suspect that 6/15 is equivalent to 2/5, you can cross-multiply:
2 x 15 = 30 6 x 5 = 30
Since the products are equal, the fractions are equivalent. This technique is particularly useful when comparing two fractions to determine if they represent the same value.
Applications of Equivalent Fractions
Equivalent fractions have wide-ranging applications in various mathematical contexts and real-world scenarios:
1. Adding and Subtracting Fractions
To add or subtract fractions, they must have a common denominator. Finding equivalent fractions with a common denominator is essential for this operation. For example, adding 1/2 and 1/4 requires finding an equivalent fraction for 1/2 with a denominator of 4:
1/2 = 2/4
Now we can add: 2/4 + 1/4 = 3/4
2. Comparing Fractions
Equivalent fractions simplify the comparison of fractions. To compare 2/5 and 3/10, you can find an equivalent fraction for 2/5 with a denominator of 10:
2/5 = 4/10
Now it's clear that 4/10 (or 2/5) is greater than 3/10.
3. Solving Equations
Equivalent fractions often appear in solving algebraic equations involving fractions. Manipulating fractions to find equivalent forms can help simplify the equation and solve for the unknown variable.
4. Real-World Applications
Equivalent fractions are used in many everyday situations:
- Cooking: If a recipe calls for 1/2 cup of sugar, and you only have a 1/4 cup measuring cup, you know you need two 1/4 cups (equivalent to 1/2 cup).
- Measurement: Converting between units of measurement (inches to feet, centimeters to meters) often involves working with equivalent fractions.
- Ratio and Proportion: Understanding equivalent fractions is crucial for working with ratios and proportions, frequently used in fields like engineering, finance, and science.
Generating Infinite Equivalent Fractions
It's important to emphasize that there are infinitely many fractions equivalent to 2/5. By multiplying the numerator and denominator by any non-zero whole number, you can generate a new equivalent fraction. This concept highlights the rich mathematical structure inherent in equivalent fractions.
Conclusion: The Power of Equivalent Fractions
The question of which fraction is equivalent to 2/5 has led us on a journey to understand the fundamental concept of equivalent fractions. We've explored various methods for finding them, visualized their meaning, and highlighted their significant role in various mathematical operations and real-world applications. Understanding equivalent fractions is a cornerstone of mathematical fluency and empowers us to solve problems across various disciplines. Mastering this concept lays a strong foundation for more advanced mathematical concepts and problem-solving skills. The ability to effortlessly manipulate and identify equivalent fractions opens doors to a deeper understanding of numbers and their relationships.
Latest Posts
Latest Posts
-
Monthly Vs Bi Weekly Vs Weekly Mortgage Calculator
May 13, 2025
-
How To Find A Missing Side Of A Rectangle
May 13, 2025
-
Greatest Common Factor Of 4 And 9
May 13, 2025
-
Z Score For 92 Confidence Interval
May 13, 2025
-
How Much Is 2 5 Percent Raise
May 13, 2025
Related Post
Thank you for visiting our website which covers about Which Fraction Is Equivalent To 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.