Which Fraction Is Equivalent To 4/6
Treneri
May 14, 2025 · 5 min read
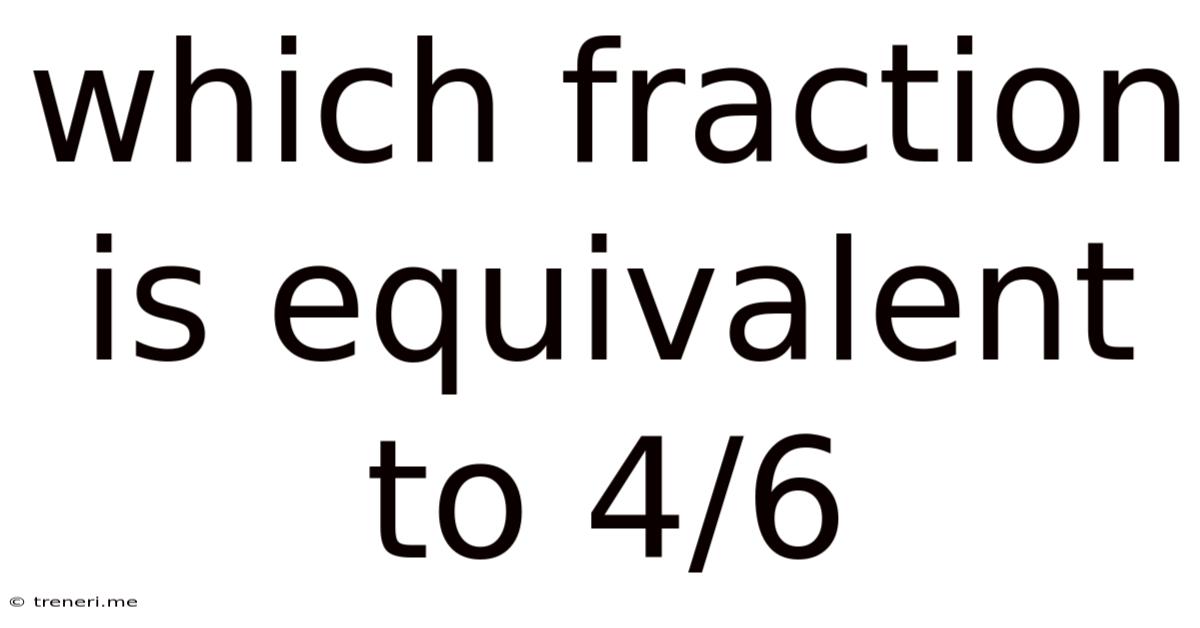
Table of Contents
Which Fraction is Equivalent to 4/6? A Deep Dive into Equivalent Fractions
Finding equivalent fractions might seem like a simple task, especially for younger learners. However, understanding the concept of equivalent fractions is crucial for mastering more advanced mathematical concepts like adding and subtracting fractions, simplifying expressions, and even grasping the fundamentals of algebra and calculus. This article will not only answer the question, "Which fraction is equivalent to 4/6?" but will also provide a comprehensive exploration of equivalent fractions, encompassing various methods for finding them, explaining the underlying principles, and offering practical examples to solidify your understanding.
Understanding Equivalent Fractions: The Core Concept
Equivalent fractions represent the same portion or value, even though they appear different. They represent the same point on a number line. Think of it like slicing a pizza: if you have a pizza cut into 6 slices and you take 4, you have the same amount of pizza as if you had a pizza cut into 12 slices and took 8. Both represent 2/3 of the pizza. The key is that the relationship between the numerator (the top number) and the denominator (the bottom number) remains constant.
The Fundamental Principle: To create an equivalent fraction, you multiply or divide both the numerator and the denominator by the same non-zero number. This ensures that the ratio between the numerator and the denominator remains unchanged, thereby maintaining the same value.
Finding Equivalent Fractions: Methods and Examples
Several methods can be employed to determine equivalent fractions. Let's delve into these methods, illustrating each with practical examples.
1. Multiplying the Numerator and Denominator:
This is the most straightforward method. To find an equivalent fraction of 4/6, you simply multiply both the numerator (4) and the denominator (6) by the same number.
-
Example 1: Multiplying by 2:
- (4 x 2) / (6 x 2) = 8/12. Therefore, 8/12 is equivalent to 4/6.
-
Example 2: Multiplying by 3:
- (4 x 3) / (6 x 3) = 12/18. Therefore, 12/18 is equivalent to 4/6.
-
Example 3: Multiplying by 5:
- (4 x 5) / (6 x 5) = 20/30. Therefore, 20/30 is equivalent to 4/6.
You can continue this process infinitely, generating an endless sequence of equivalent fractions for 4/6.
2. Dividing the Numerator and Denominator:
This method is used to simplify a fraction to its lowest terms, also known as simplifying or reducing the fraction. To do this, you find the greatest common divisor (GCD) of the numerator and the denominator and divide both by that GCD.
The GCD of 4 and 6 is 2.
- Dividing by the GCD:
- (4 ÷ 2) / (6 ÷ 2) = 2/3. Therefore, 2/3 is the simplest equivalent fraction of 4/6.
3. Using Visual Aids: Fraction Bars and Circles
Visual aids can be incredibly helpful, particularly for beginners. Drawing fraction bars or circles representing the fraction 4/6 and then dividing or grouping the sections to illustrate equivalent fractions is a very effective approach. For example, you could divide a rectangle into 6 equal parts, shade 4, and then show how this is equivalent to 2/3 by grouping the shaded parts.
Why is Understanding Equivalent Fractions Important?
The ability to identify and manipulate equivalent fractions is fundamental to a strong understanding of mathematics and its applications. Here's why:
-
Simplifying Fractions: Reducing fractions to their simplest form improves clarity and makes calculations easier. For instance, 12/18 is more cumbersome to work with than its simplified equivalent, 2/3.
-
Adding and Subtracting Fractions: Before adding or subtracting fractions, you need to find a common denominator—a denominator that's a multiple of both denominators. This often involves finding equivalent fractions.
-
Comparing Fractions: Determining which of two fractions is larger or smaller requires a common denominator. Converting fractions to equivalent fractions with the same denominator makes this comparison straightforward.
-
Solving Equations: Many algebraic equations involve fractions, and the ability to manipulate equivalent fractions is crucial for solving them efficiently.
-
Real-World Applications: Equivalent fractions are used in numerous real-world scenarios, including cooking (measuring ingredients), construction (measuring materials), and finance (working with percentages).
Specific Equivalent Fractions for 4/6: A Comprehensive List
Let's generate a more extensive list of fractions equivalent to 4/6, utilizing both multiplication and division. Remember, the simplest form is 2/3.
- Simplest form: 2/3
- Multiplying by 2: 8/12
- Multiplying by 3: 12/18
- Multiplying by 4: 16/24
- Multiplying by 5: 20/30
- Multiplying by 6: 24/36
- Multiplying by 7: 28/42
- Multiplying by 8: 32/48
- Multiplying by 9: 36/54
- Multiplying by 10: 40/60
This list can extend indefinitely by multiplying the numerator and denominator by any positive integer.
Beyond the Basics: Further Exploration
While this article focuses primarily on the fundamental aspects of equivalent fractions, it's important to acknowledge the more advanced concepts related to this topic. These include:
-
Ratio and Proportion: Equivalent fractions directly relate to the concept of ratio and proportion. Understanding these concepts is crucial for solving problems involving ratios, scaling, and similar figures.
-
Decimal Representation: Every fraction can be expressed as a decimal. Understanding how to convert a fraction to its decimal equivalent and vice versa is a valuable skill.
-
Percentage Representation: Percentages are simply fractions with a denominator of 100. The ability to convert fractions to percentages and vice versa is highly useful in many real-world contexts.
Conclusion: Mastering Equivalent Fractions
The concept of equivalent fractions, though seemingly basic, is a cornerstone of mathematical understanding. This article provides a thorough explanation of how to find equivalent fractions, emphasizing the importance of both multiplying and dividing the numerator and denominator by the same number. By mastering this concept, you lay a solid foundation for more advanced mathematical topics and applications. Remember the key principle: equivalent fractions represent the same portion or value, despite their different numerical representation. The methods outlined here, combined with visual aids and practice, will equip you to confidently work with equivalent fractions in any mathematical context. Through consistent practice and understanding of the underlying principles, the seemingly simple task of finding equivalent fractions will become second nature, opening up a world of mathematical possibilities.
Latest Posts
Latest Posts
-
Formula For Price Per Square Foot
May 15, 2025
-
How Long Does It Take To Burn In Uv 9
May 15, 2025
-
How Many Days Is In 16 Years
May 15, 2025
-
Cuanto Falta Para El 26 De Enero
May 15, 2025
-
Convert 25 Meters To Yards Swimming
May 15, 2025
Related Post
Thank you for visiting our website which covers about Which Fraction Is Equivalent To 4/6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.