Which Fraction Is Equivalent To 8/12
Treneri
May 10, 2025 · 5 min read
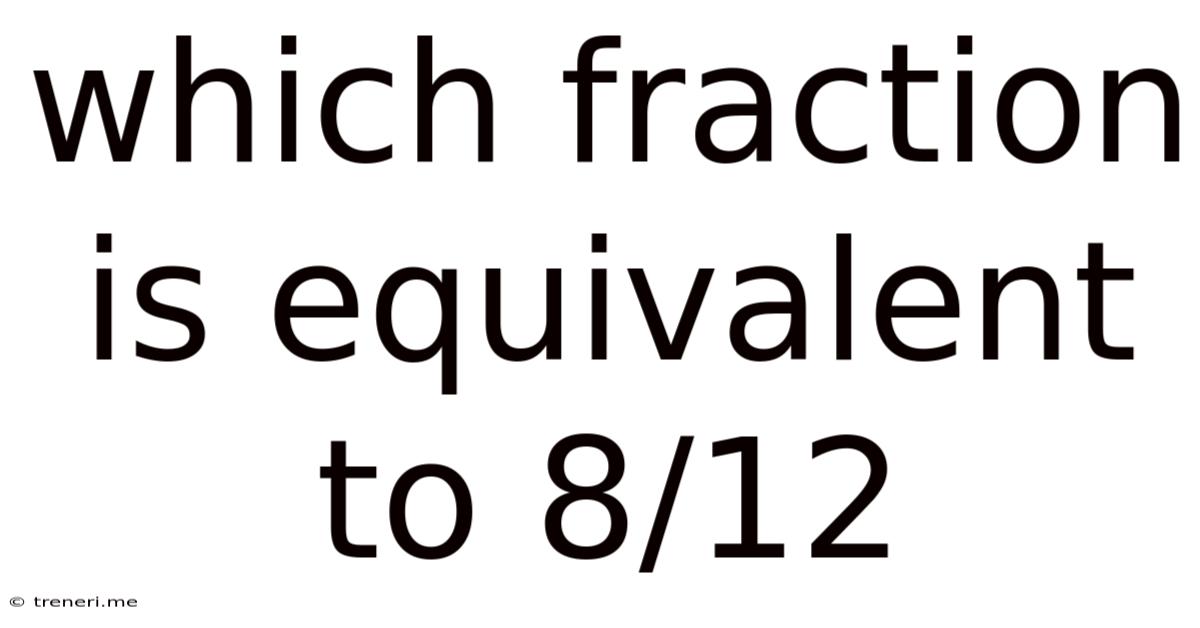
Table of Contents
Which Fraction is Equivalent to 8/12? A Deep Dive into Equivalent Fractions
Finding equivalent fractions might seem like a simple task, especially when dealing with easily reduced fractions like 8/12. However, understanding the underlying principles of equivalent fractions is crucial for mastering more complex mathematical concepts. This comprehensive guide explores various methods to determine fractions equivalent to 8/12, delves into the concept of simplifying fractions, and provides practical examples to solidify your understanding. We'll even touch upon how equivalent fractions relate to ratios and proportions, making this a complete resource for anyone looking to master this fundamental mathematical skill.
Understanding Equivalent Fractions
Equivalent fractions represent the same proportion or value, even though they look different. Think of it like slicing a pizza: If you have a pizza cut into 12 slices and you eat 8, you've eaten the same amount as if you had a pizza cut into 6 slices and eaten 4. Both represent the same portion of the whole pizza. Therefore, 8/12 and 4/6 are equivalent fractions.
The key to understanding equivalent fractions lies in the concept of multiplying or dividing both the numerator (top number) and the denominator (bottom number) by the same non-zero number. This process maintains the ratio, ensuring the resulting fraction holds the same value as the original.
Finding Equivalent Fractions by Multiplication
To find equivalent fractions, simply multiply both the numerator and the denominator by the same number. Let's start with 8/12:
- Multiply by 2: (8 x 2) / (12 x 2) = 16/24
- Multiply by 3: (8 x 3) / (12 x 3) = 24/36
- Multiply by 4: (8 x 4) / (12 x 4) = 32/48
- Multiply by 5: (8 x 5) / (12 x 5) = 40/60
And so on. You can generate an infinite number of equivalent fractions by multiplying by any whole number greater than 1.
Finding Equivalent Fractions by Division (Simplification)
The reverse process, dividing both the numerator and the denominator by the same number, is called simplification or reducing a fraction to its lowest terms. This is particularly useful for finding the simplest equivalent fraction. To simplify 8/12, we need to find the greatest common divisor (GCD) of 8 and 12.
The GCD is the largest number that divides both 8 and 12 without leaving a remainder. In this case, the GCD of 8 and 12 is 4. Dividing both the numerator and the denominator by 4:
(8 ÷ 4) / (12 ÷ 4) = 2/3
Therefore, 2/3 is the simplest equivalent fraction to 8/12. It represents the same proportion but uses the smallest possible whole numbers.
Methods to Find the Greatest Common Divisor (GCD)
Finding the GCD is crucial for simplifying fractions. Here are two common methods:
1. Listing Factors
List all the factors (numbers that divide evenly) of both the numerator and the denominator:
- Factors of 8: 1, 2, 4, 8
- Factors of 12: 1, 2, 3, 4, 6, 12
The largest number that appears in both lists is 4, which is the GCD.
2. Prime Factorization
Break down both numbers into their prime factors (numbers divisible only by 1 and themselves):
- 8 = 2 x 2 x 2 = 2³
- 12 = 2 x 2 x 3 = 2² x 3
The common prime factors are 2 x 2 = 4. Therefore, the GCD is 4.
Visual Representation of Equivalent Fractions
Visual aids can significantly enhance understanding. Imagine a rectangle divided into 12 equal parts. Shading 8 of these parts represents the fraction 8/12. Now, imagine grouping those shaded parts into larger sections. You could group them into 2 groups of 4, representing 4/6 (dividing the original rectangle into 6 sections). Similarly, you could group them into 1 group of 8, representing 2/3 (dividing the rectangle into only 3 sections). These visual groupings demonstrate the equivalence of the fractions.
Equivalent Fractions and Ratios
Equivalent fractions are fundamentally linked to ratios. A ratio compares two quantities. For instance, the ratio of shaded to unshaded parts in our 8/12 example is 8:4, which simplifies to 2:1. This ratio is identical to the ratio represented by the simplified fraction 2/3. Understanding this connection strengthens the understanding of both concepts.
Equivalent Fractions and Proportions
Proportions state that two ratios are equal. For example, 8/12 = 2/3 is a proportion. Cross-multiplication can verify this: (8 x 3) = (12 x 2) = 24. This property is fundamental in solving problems involving proportions and scaling.
Real-World Applications of Equivalent Fractions
Equivalent fractions are not merely abstract mathematical concepts; they have numerous practical applications:
- Cooking: If a recipe calls for 2/3 cup of sugar, and you only have a 1/4 cup measuring cup, you'll need to figure out the equivalent fraction to measure the correct amount.
- Construction: Scaling blueprints accurately requires understanding equivalent fractions.
- Sewing: Calculating fabric amounts for projects often involves working with fractions and their equivalents.
- Data Analysis: Representing data proportions clearly and concisely involves simplifying fractions to their lowest terms.
Solving Problems Involving Equivalent Fractions
Let's solidify your understanding with a few examples:
Example 1: A pizza is cut into 24 slices. If you eat 16 slices, what fraction of the pizza did you eat? Simplify your answer.
- Fraction eaten: 16/24
- GCD of 16 and 24 is 8.
- Simplified fraction: (16 ÷ 8) / (24 ÷ 8) = 2/3 You ate 2/3 of the pizza.
Example 2: Are 15/20 and 3/4 equivalent fractions?
- Simplify 15/20: GCD of 15 and 20 is 5. (15 ÷ 5) / (20 ÷ 5) = 3/4
- Since both fractions simplify to 3/4, they are equivalent.
Example 3: Find three equivalent fractions to 5/7.
- Multiply by 2: (5 x 2) / (7 x 2) = 10/14
- Multiply by 3: (5 x 3) / (7 x 3) = 15/21
- Multiply by 4: (5 x 4) / (7 x 4) = 20/28
Conclusion
Understanding equivalent fractions is a cornerstone of mathematical proficiency. Mastering the techniques of finding the GCD, simplifying fractions, and applying these concepts to ratios and proportions opens the door to a deeper understanding of more complex mathematical ideas. The ability to work confidently with fractions is invaluable in numerous real-world applications, making it a skill worth mastering. Remember to practice regularly; the more you work with fractions, the more intuitive the process will become.
Latest Posts
Latest Posts
-
How Many Minutes Until 12 00 Am
May 10, 2025
-
60 Days Before October 10 2024
May 10, 2025
-
41 Rounded To The Nearest Ten
May 10, 2025
-
4 3 To The Power Of 3
May 10, 2025
-
Cuanto Es 11 Libras En Kg
May 10, 2025
Related Post
Thank you for visiting our website which covers about Which Fraction Is Equivalent To 8/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.