Which Fractions Are Equivalent To 10/12
Treneri
May 14, 2025 · 5 min read
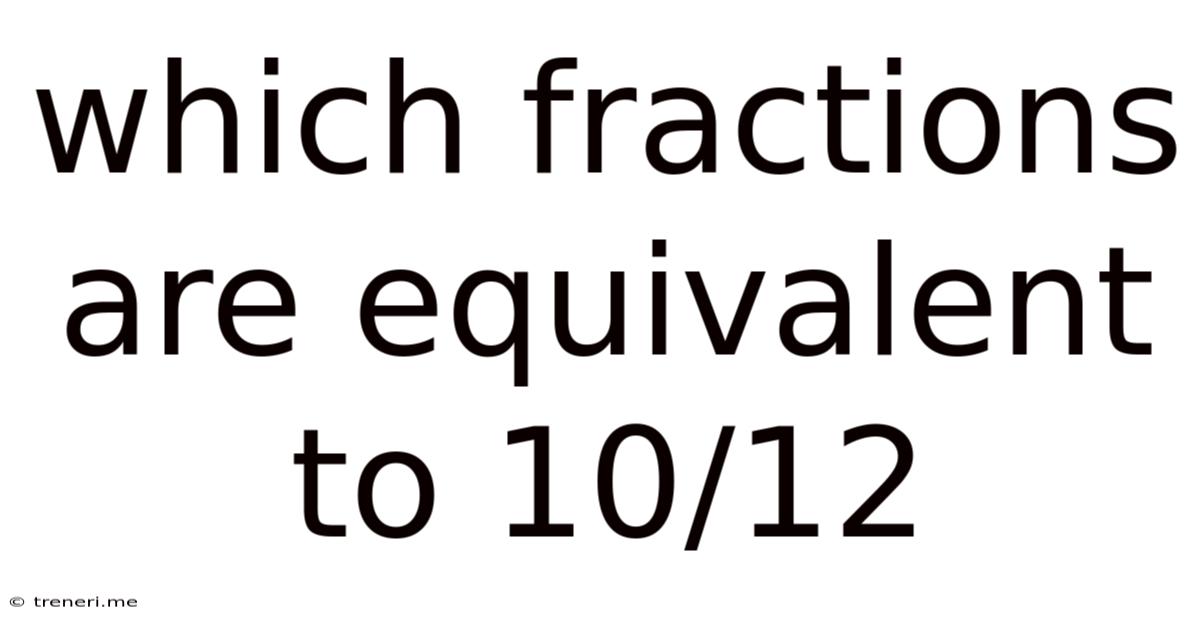
Table of Contents
Which Fractions are Equivalent to 10/12? A Comprehensive Guide
Finding equivalent fractions might seem like a simple task, but understanding the underlying principles is crucial for mastering fractions and related mathematical concepts. This comprehensive guide delves into the world of equivalent fractions, focusing specifically on fractions equivalent to 10/12. We'll explore various methods for finding these equivalents, explain the underlying mathematical reasoning, and provide practical examples to solidify your understanding.
Understanding Equivalent Fractions
Equivalent fractions represent the same portion or value, even though they look different. Imagine slicing a pizza: one half (1/2) is the same as two quarters (2/4) or four eighths (4/8). These are all equivalent fractions. The key principle is that you can multiply or divide both the numerator (top number) and the denominator (bottom number) of a fraction by the same non-zero number without changing its value.
Methods for Finding Equivalent Fractions to 10/12
There are several approaches to identify fractions equivalent to 10/12:
1. Simplifying the Fraction (Finding the Simplest Form)
The most common method involves simplifying the fraction to its simplest form. This involves finding the greatest common divisor (GCD) of the numerator (10) and the denominator (12). The GCD is the largest number that divides both 10 and 12 without leaving a remainder.
Finding the GCD:
The factors of 10 are 1, 2, 5, and 10. The factors of 12 are 1, 2, 3, 4, 6, and 12.
The greatest common factor of 10 and 12 is 2.
Simplifying:
Divide both the numerator and the denominator by the GCD (2):
10 ÷ 2 = 5 12 ÷ 2 = 6
Therefore, the simplest form of 10/12 is 5/6.
2. Multiplying the Numerator and Denominator
Once you have the simplest form (5/6), you can generate other equivalent fractions by multiplying both the numerator and the denominator by the same number. Let's try multiplying by 2, 3, 4, and 5:
- Multiply by 2: (5 x 2) / (6 x 2) = 10/12 (This confirms our starting point!)
- Multiply by 3: (5 x 3) / (6 x 3) = 15/18
- Multiply by 4: (5 x 4) / (6 x 4) = 20/24
- Multiply by 5: (5 x 5) / (6 x 5) = 25/30
And so on. You can continue this process indefinitely, generating an infinite number of equivalent fractions.
3. Dividing the Numerator and Denominator (Less Common for this Fraction)
While less applicable to 10/12 because it's already in a relatively simplified form, this method is crucial for understanding the concept. If you had a larger fraction, you could divide both the numerator and denominator by a common factor. For instance, if you started with 20/24, you could divide by 4 to get 5/6.
Visualizing Equivalent Fractions
Visual aids can significantly improve understanding. Imagine a rectangular shape representing a whole.
- 10/12: Divide the rectangle into 12 equal parts and shade 10 of them.
- 5/6: Divide a different rectangle into 6 equal parts and shade 5 of them. You'll see that the shaded area is visually identical, confirming that 10/12 and 5/6 are equivalent. You can apply this to 15/18, 20/24, etc., always arriving at the same visual representation of the shaded area.
The Importance of Equivalent Fractions
Understanding equivalent fractions is foundational to many mathematical concepts:
- Adding and Subtracting Fractions: You need to find a common denominator (a common bottom number) before adding or subtracting fractions. This often involves finding equivalent fractions.
- Comparing Fractions: Determining which of two fractions is larger or smaller can be easier after simplifying them or finding equivalent fractions with a common denominator.
- Ratio and Proportion: Equivalent fractions are directly related to ratios and proportions. Understanding them is essential in solving problems involving scaling, mixing ingredients, or similar applications.
- Decimals and Percentages: Converting fractions to decimals and percentages frequently involves simplifying fractions or finding equivalent fractions with denominators like 10, 100, or 1000.
Practical Applications
Equivalent fractions aren't just abstract mathematical concepts. They pop up in everyday situations:
- Cooking: A recipe calls for 1/2 cup of sugar, but you only have a 1/4 cup measuring cup. Knowing that 1/2 is equivalent to 2/4, you know you need to use two 1/4 cups.
- Construction: Dividing lengths or materials accurately often requires working with fractions and their equivalents.
- Finance: Calculating proportions of income, expenses, or investments requires a solid understanding of fractions and their equivalents.
- Data Analysis: Representing data visually using charts and graphs frequently relies on fractions and the ability to manipulate and compare them.
Beyond 10/12: A Broader Perspective
The principles discussed for 10/12 apply to any fraction. To find equivalent fractions for any given fraction:
- Simplify: Find the GCD of the numerator and denominator and divide both by it.
- Multiply: Multiply both the numerator and denominator by the same whole number (greater than 1) to create new equivalent fractions.
- Visualize: Use diagrams or models to represent the fraction visually, confirming equivalence.
Common Mistakes to Avoid
- Only multiplying or dividing the numerator or denominator: Remember, you must always perform the same operation (multiplication or division) on both the numerator and the denominator.
- Using zero as a multiplier or divisor: Dividing by zero is undefined in mathematics.
- Not simplifying to the simplest form: While not always necessary, simplifying a fraction to its simplest form often makes it easier to work with and understand.
Conclusion
Understanding equivalent fractions is a cornerstone of mathematical fluency. By mastering the techniques outlined in this guide, you'll gain confidence in working with fractions and apply this knowledge to various real-world scenarios. Remember the key principles: simplification using the GCD, and multiplying or dividing both the numerator and denominator by the same non-zero number. Practice makes perfect, so keep working with different fractions and visualizing their equivalence to strengthen your understanding. The ability to easily identify and manipulate equivalent fractions will serve you well in countless mathematical endeavors.
Latest Posts
Latest Posts
-
Gestation Period For Sheep In Months
May 14, 2025
-
9 30 To 3 30 Is How Many Hours
May 14, 2025
-
What Is The Greatest Common Factor Of 52 And 26
May 14, 2025
-
What Percent Is 24 Out Of 25
May 14, 2025
-
What Is The Greatest Common Factor Of 6 And 14
May 14, 2025
Related Post
Thank you for visiting our website which covers about Which Fractions Are Equivalent To 10/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.