X 1 2 In Radical Form
Treneri
May 13, 2025 · 5 min read
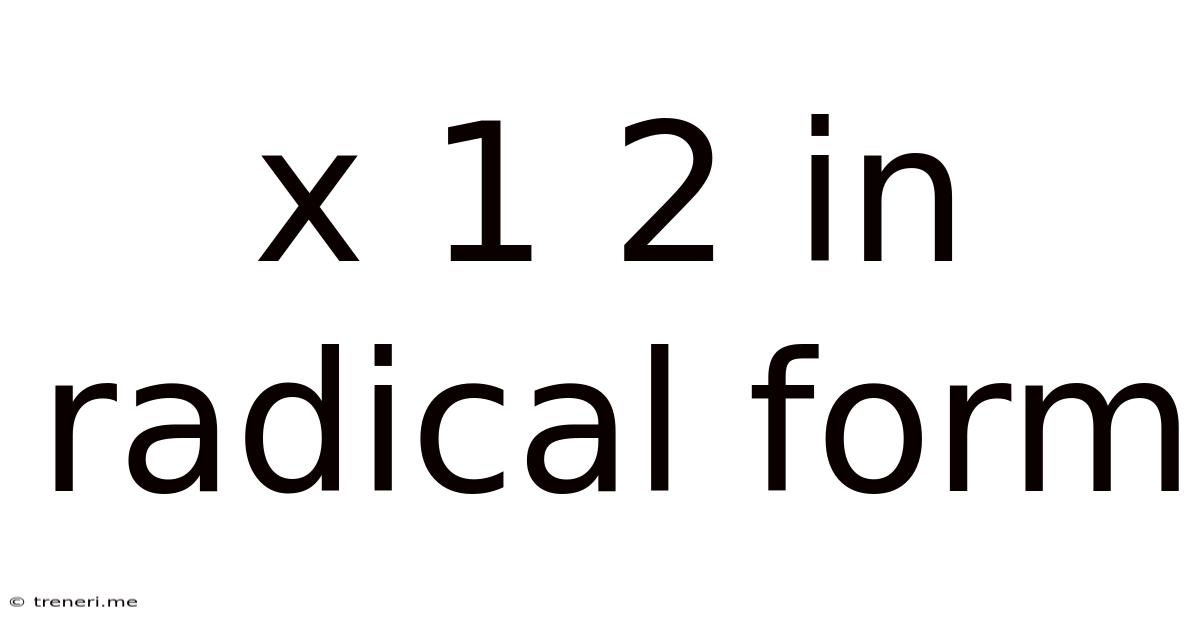
Table of Contents
x¹⁄₂ in Radical Form: A Comprehensive Guide
Understanding how to express exponents as radicals is a fundamental concept in algebra. This comprehensive guide will explore the intricacies of representing x¹⁄₂ in radical form, along with related concepts and examples to solidify your understanding. We'll cover not only the basic conversion but also delve into more complex scenarios, addressing common misconceptions and providing practical applications.
Understanding Exponents and Radicals
Before diving into the specific conversion of x¹⁄₂, let's review the core concepts of exponents and radicals. These two mathematical representations are intrinsically linked, serving as different ways to express the same underlying mathematical operation.
Exponents: A Quick Refresher
Exponents, often called powers or indices, indicate repeated multiplication. For instance, x³ means x * x * x. The base (x) is the number being multiplied, and the exponent (3) denotes how many times the base is multiplied by itself. Fractional exponents introduce a new dimension to this concept.
Radicals: Unveiling the Root
Radicals represent roots. The most common radical is the square root (√), which signifies finding a number that, when multiplied by itself, yields the number under the radical sign (radicand). Cube roots (∛), fourth roots, and so on, extend this concept to higher powers. The small number preceding the radical sign (the index) indicates the root being taken. For example:
- √x (or x¹⁄²) is the square root of x.
- ∛x (or x¹⁄³) is the cube root of x.
- ⁴√x (or x¹⁄⁴) is the fourth root of x.
Converting x¹⁄₂ to Radical Form
The expression x¹⁄₂ represents a fractional exponent. To convert this into radical form, we utilize the relationship between exponents and radicals:
x^(m/n) = ⁿ√xᵐ
In our case, m = 1 and n = 2. Therefore, applying this rule, we get:
x¹⁄₂ = √x
This means that x¹⁄₂ is equivalent to the square root of x. This fundamental conversion is the cornerstone of many algebraic manipulations and problem-solving techniques.
Exploring Variations and Complexities
While the basic conversion of x¹⁄₂ is straightforward, the concept extends to more complex scenarios involving negative exponents, different fractional exponents, and expressions within the base.
Negative Exponents
A negative exponent implies a reciprocal. For instance, x⁻² = 1/x². This principle extends to fractional exponents as well. Consider x⁻¹⁄₂. Following the rules of exponents and radicals:
x⁻¹⁄₂ = 1/x¹⁄₂ = 1/√x
This demonstrates that a negative fractional exponent results in the reciprocal of the corresponding positive fractional exponent in radical form.
Higher-Order Fractional Exponents
The conversion principle applies equally well to fractional exponents other than ½. For example:
- x²/³ = ∛x² (the cube root of x squared)
- x⁵⁄₄ = ⁴√x⁵ (the fourth root of x to the power of 5)
- x⁷⁄² = √x⁷ (the square root of x to the power of 7)
In each case, the numerator of the fractional exponent becomes the power of the base within the radical, and the denominator determines the root being taken.
Expressions within the Base
The base of the exponent doesn't have to be a single variable. It can be an expression. For example:
(a + b)¹⁄₂ = √(a + b)
This shows that the entire expression (a + b) is under the square root. Remember to treat the parentheses carefully when dealing with expressions as the base.
Combining Concepts
More complex scenarios might require combining multiple concepts. For example:
(4x²y)¹⁄² = √(4x²y) = 2x√y
This example combines a fractional exponent with algebraic simplification. Note that we can simplify √(4x²) to 2x because the square root of 4 is 2 and the square root of x² is x (assuming x is non-negative).
Practical Applications and Problem-Solving
Understanding the conversion between fractional exponents and radicals is crucial for various mathematical applications:
Simplifying Expressions
Converting between exponential and radical forms often simplifies algebraic expressions, making them easier to manipulate and solve. This is particularly useful in calculus and other advanced mathematical fields.
Solving Equations
Many equations involving radicals can be simplified by converting them to exponential form, facilitating the application of exponential rules to solve for the unknown variable.
Calculus
The concept is fundamental to differential and integral calculus, where derivatives and integrals of functions involving roots often require converting between radical and exponential forms for easier computation.
Geometry and Trigonometry
Many geometric formulas and trigonometric identities involve square roots and other radicals, showcasing the practical application of converting between these forms.
Common Mistakes to Avoid
Several common mistakes can hinder the understanding and application of converting x¹⁄₂ and similar expressions to radical form:
- Misinterpreting the index: Remember that the denominator of the fractional exponent determines the root (index of the radical). A common mistake is to confuse the numerator and denominator.
- Incorrect simplification: Always ensure proper simplification of the radical expression after conversion. Factoring and using the properties of radicals are crucial for obtaining the most simplified form.
- Neglecting parentheses: When dealing with expressions as the base, parentheses are crucial to ensure the correct scope of the exponent. Omitting parentheses can lead to incorrect results.
Advanced Concepts: Extending the Understanding
For those wanting to delve deeper, here are some advanced concepts related to fractional exponents and radicals:
- Rationalizing the denominator: A technique used to remove radicals from the denominator of a fraction. This involves multiplying the numerator and denominator by a suitable expression to eliminate the radical from the denominator.
- Complex numbers: Fractional exponents can be extended to complex numbers, opening up a whole new dimension of mathematical exploration.
- Nth roots of unity: These are complex numbers that, when raised to the power of n, result in 1. Understanding these concepts requires a good grasp of complex numbers and fractional exponents.
Conclusion: Mastering the Conversion
Mastering the conversion of x¹⁄₂ to its radical form, √x, is a fundamental step in advanced mathematical studies. Understanding the underlying principles of exponents and radicals, and practicing various examples, solidifies this understanding. By avoiding common pitfalls and exploring advanced concepts, you will develop a strong foundation in algebra and prepare for more complex mathematical challenges ahead. Remember, consistent practice and a thorough understanding of the underlying principles are key to success in this area. Continue to explore different variations and problem sets to solidify your understanding and build confidence in tackling even more challenging problems involving fractional exponents and radicals.
Latest Posts
Latest Posts
-
Cuanto Es 3 Cuartos De Agua
May 14, 2025
-
Cuanta Leche Consume Un Recien Nacido
May 14, 2025
-
What Is The Greatest Common Factor Of 12 And 54
May 14, 2025
-
How Long Is 1 Million Seconds In Days
May 14, 2025
-
What Is A Equivalent Fraction For 6 8
May 14, 2025
Related Post
Thank you for visiting our website which covers about X 1 2 In Radical Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.