X 2 3 In Radical Form
Treneri
May 09, 2025 · 4 min read
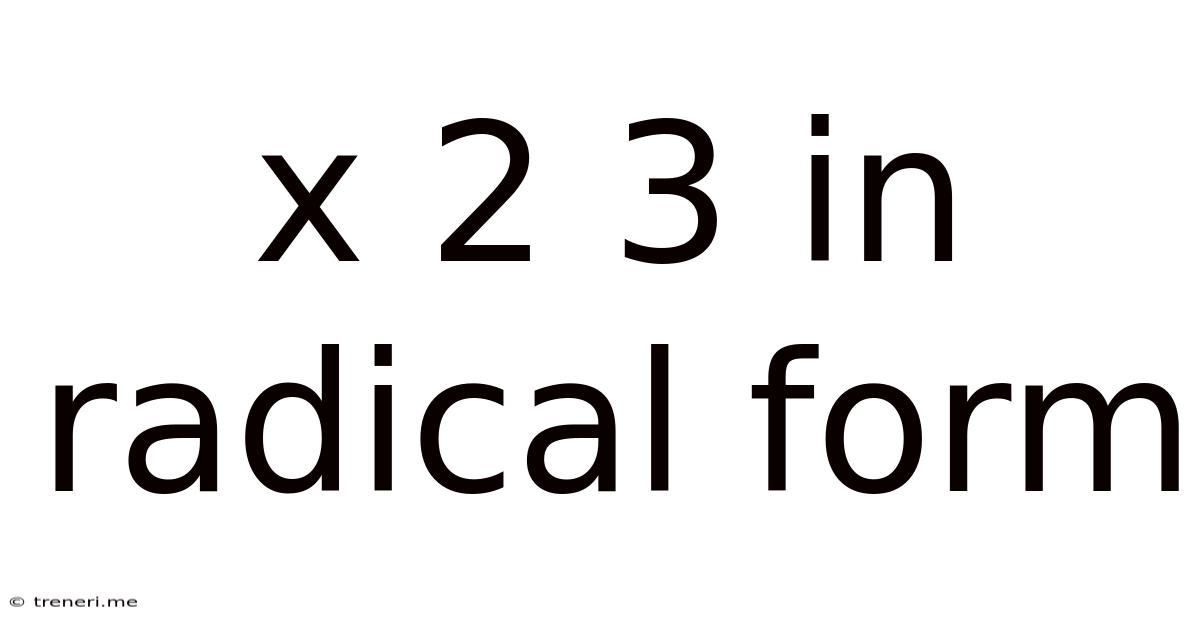
Table of Contents
x²⁄³ in Radical Form: A Comprehensive Guide
Understanding how to express exponential expressions, particularly those involving fractional exponents, in radical form is crucial for success in algebra and beyond. This comprehensive guide will delve into the intricacies of expressing x²⁄³ in radical form, exploring the underlying principles and providing you with a solid understanding of the process. We will also examine related concepts and provide you with various examples to solidify your grasp of the topic.
Understanding Fractional Exponents
Before we tackle x²⁄³, let's review the fundamental relationship between exponents and radicals. A fractional exponent signifies both exponentiation and root extraction. The numerator of the fraction represents the power to which the base is raised, while the denominator indicates the root to be taken. In general terms:
x<sup>m/n</sup> = <sup>n</sup>√(x<sup>m</sup>) = (<sup>n</sup>√x)<sup>m</sup>
Where:
- x is the base
- m is the exponent (power)
- n is the root (index of the radical)
This formula is the cornerstone of converting between exponential and radical notation.
Expressing x²⁄³ in Radical Form
Applying the above formula to x²⁄³, we have:
x<sup>2/3</sup> = <sup>3</sup>√(x²) = (<sup>3</sup>√x)²
This means that x raised to the power of two-thirds is equivalent to the cube root of x squared, or the square of the cube root of x. Both expressions are mathematically identical and represent the same value. The choice between them often depends on the context and the specific calculation being performed. Sometimes one form is simpler to work with than the other.
Detailed Breakdown of the Conversion
Let's break down the conversion step-by-step to enhance understanding:
-
Identify the Numerator and Denominator: In the exponent 2/3, the numerator is 2, and the denominator is 3.
-
Determine the Root: The denominator (3) represents the index of the radical, indicating a cube root (<sup>3</sup>√).
-
Determine the Power: The numerator (2) represents the exponent to which the base (x) is raised, indicating that x is squared (x²).
-
Apply the Formula: Substitute these values into the general formula: x<sup>m/n</sup> = <sup>n</sup>√(x<sup>m</sup>). This yields <sup>3</sup>√(x²).
Alternative Radical Form: (<sup>3</sup>√x)²
The expression can also be written as (<sup>3</sup>√x)². This form is equally valid and demonstrates that we can either square x first and then take the cube root, or take the cube root of x first and then square the result. The order of operations in this case does not affect the final outcome.
Illustrative Examples
Let's illustrate the concept with numerical examples. Consider the case where x = 8:
x<sup>2/3</sup> = 8<sup>2/3</sup>
Using the radical form:
<sup>3</sup>√(8²) = <sup>3</sup>√(64) = 4
Alternatively, using the other radical form:
(<sup>3</sup>√8)² = (2)² = 4
As you can see, both methods produce the same result, confirming the equivalence of the two radical expressions.
Exploring Further: Negative Fractional Exponents
Our understanding extends to negative fractional exponents. Recall that a negative exponent signifies the reciprocal of the positive exponent:
x<sup>-m/n</sup> = 1 / x<sup>m/n</sup>
Therefore, x<sup>-2/3</sup> would be expressed as:
x<sup>-2/3</sup> = 1 / x<sup>2/3</sup> = 1 / <sup>3</sup>√(x²) = 1 / (<sup>3</sup>√x)²
Dealing with Complex Bases
The principle remains the same even when the base is more complex than a single variable. For example, if the base is (2y) instead of just x:
(2y)<sup>2/3</sup> = <sup>3</sup>√((2y)²) = <sup>3</sup>√(4y²) = (<sup>3</sup>√(2y))²
Simplifying Radical Expressions
Often, you'll need to simplify the resulting radical expressions. This involves factoring and extracting perfect roots. For example, if you have:
<sup>3</sup>√(8x³)
You can simplify this by factoring:
<sup>3</sup>√(2³ * x³) = 2x
Applications of Fractional Exponents and Radicals
Fractional exponents and their radical representations have widespread applications in various fields, including:
- Calculus: They are essential for differentiation and integration.
- Physics: They appear in formulas describing motion, waves, and other physical phenomena.
- Engineering: Used extensively in structural analysis, fluid mechanics, and electrical engineering.
- Finance: They're crucial for compound interest calculations.
Conclusion
Expressing x²⁄³ in radical form, as either <sup>3</sup>√(x²) or (<sup>3</sup>√x)², is a fundamental skill in algebra and a gateway to a deeper understanding of exponents and radicals. This guide provided a detailed explanation, complete with illustrative examples, ensuring a solid grasp of the conversion process. Remember the crucial formula connecting exponential and radical notation: x<sup>m/n</sup> = <sup>n</sup>√(x<sup>m</sup>) = (<sup>n</sup>√x)<sup>m</sup>. By mastering this concept, you'll be well-equipped to handle more complex mathematical problems and confidently navigate various scientific and engineering applications. Consistent practice with different examples is key to developing proficiency in manipulating fractional exponents and simplifying radical expressions.
Latest Posts
Latest Posts
-
1 Stick Margarine To Oil Conversion
May 11, 2025
-
450 Grams Is How Many Ounces
May 11, 2025
-
What Is 9 Out Of 13 As A Grade
May 11, 2025
-
How Many Seconds Is 25 Minutes
May 11, 2025
-
How Many Milliseconds In 10 Seconds
May 11, 2025
Related Post
Thank you for visiting our website which covers about X 2 3 In Radical Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.