X Is Y Percent Of Z
Treneri
Apr 20, 2025 · 4 min read
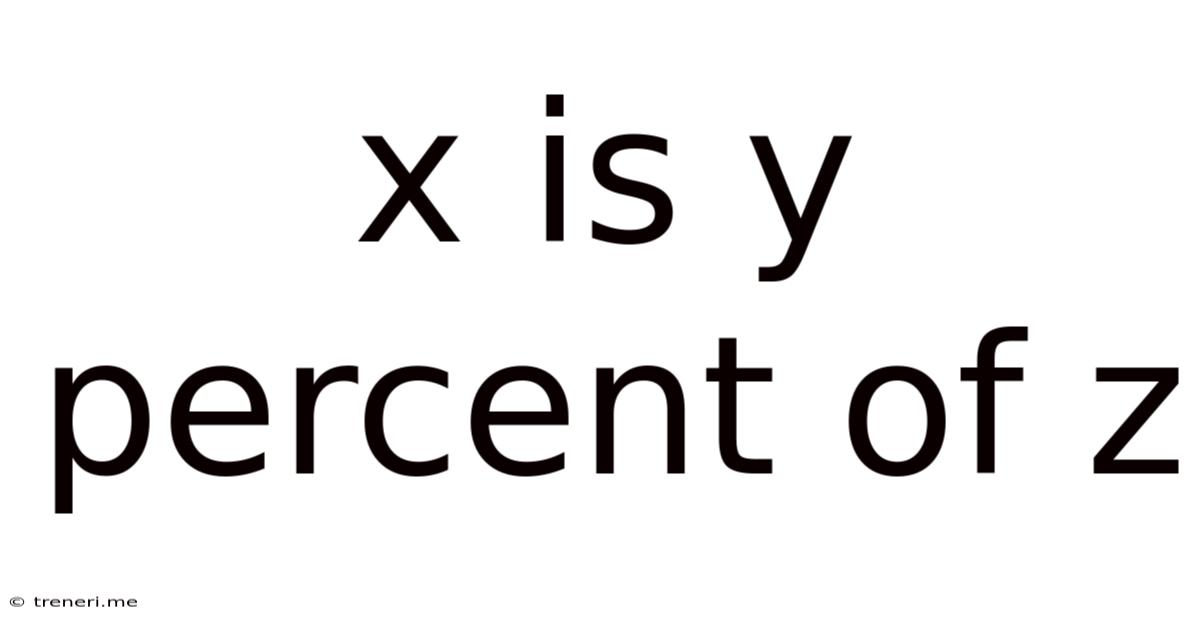
Table of Contents
X is Y Percent of Z: Mastering Percentage Calculations
Percentages are fundamental to everyday life, whether you're calculating discounts at the mall, understanding financial reports, or analyzing data for work. Understanding how to solve problems framed as "X is Y percent of Z" is a crucial skill. This comprehensive guide will delve into the meaning of this statement, explore different approaches to solving such problems, provide practical examples, and even touch upon advanced applications.
Understanding the Core Concept
The statement "X is Y percent of Z" represents a fundamental relationship between three quantities:
- X: This represents the resulting part or portion. It's the value you're trying to find or already know.
- Y: This is the percentage, expressed as a number (e.g., 25 instead of 25%).
- Z: This represents the whole or total value from which the percentage is taken.
Essentially, the statement describes a proportion: X is a fraction (Y/100) of Z.
Different Approaches to Solving for X, Y, or Z
The beauty of this equation is its versatility. You can solve for any of the three variables (X, Y, or Z) if you know the other two. Let's break down each scenario:
1. Solving for X (Finding the Part):
This is the most common application. The formula is straightforward:
X = (Y/100) * Z
Example: What is 20% of 50?
Here, Y = 20, and Z = 50. Plugging these values into the formula:
X = (20/100) * 50 = 10
Therefore, 10 is 20% of 50.
2. Solving for Y (Finding the Percentage):
This involves determining what percentage one number represents of another. The formula is:
Y = (X/Z) * 100
Example: 15 is what percent of 75?
Here, X = 15, and Z = 75. Applying the formula:
Y = (15/75) * 100 = 20
Therefore, 15 is 20% of 75.
3. Solving for Z (Finding the Whole):
This involves determining the total value given a part and its percentage. The formula is:
Z = (X * 100) / Y
Example: 25 is 50% of what number?
Here, X = 25, and Y = 50. Using the formula:
Z = (25 * 100) / 50 = 50
Therefore, 25 is 50% of 50.
Practical Applications and Real-World Examples
The "X is Y percent of Z" formula finds extensive use in various contexts:
1. Finance and Budgeting:
- Calculating discounts: A store offers a 30% discount on a $100 item. X (the discount amount) = (30/100) * $100 = $30.
- Determining interest earned: If you earn 5% interest on a $1000 savings account, your interest (X) = (5/100) * $1000 = $50.
- Analyzing financial statements: Understanding profit margins, revenue growth percentages, and expense ratios all rely on percentage calculations.
2. Sales and Marketing:
- Conversion rates: If 1000 people visit a website and 100 make a purchase, the conversion rate (Y) = (100/1000) * 100 = 10%.
- Market share analysis: Determining a company's share of a total market requires percentage calculations.
- Analyzing campaign performance: Tracking click-through rates, engagement rates, and other key metrics involves understanding percentages.
3. Everyday Life:
- Calculating tips: A 15% tip on a $50 meal is (15/100) * $50 = $7.50.
- Understanding tax rates: Calculating sales tax or income tax often involves determining a percentage of a total amount.
- Recipe scaling: Adjusting ingredient quantities in a recipe by a certain percentage.
Advanced Applications and Considerations
Beyond the basic calculations, understanding percentages extends to more complex scenarios:
1. Percentage Change:
This involves calculating the increase or decrease in a value relative to its original value. The formula is:
Percentage Change = [(New Value - Old Value) / Old Value] * 100
Example: A stock price increased from $50 to $60. The percentage change = [(60 - 50) / 50] * 100 = 20%.
2. Compound Interest:
Compound interest involves earning interest on both the principal amount and accumulated interest. The formula is slightly more complex, involving exponents.
3. Statistical Analysis:
Percentages are crucial in various statistical analyses, including hypothesis testing, confidence intervals, and regression analysis.
Tips and Tricks for Accurate Calculations
- Use a calculator: For complex calculations, a calculator ensures accuracy.
- Convert percentages to decimals: Dividing the percentage by 100 simplifies calculations (e.g., 25% = 0.25).
- Check your work: Verify your answers by using alternative methods or estimations.
- Understand the context: Always consider the meaning of the numbers involved to ensure your calculations are relevant.
Conclusion: Mastering Percentages for Success
The ability to confidently solve problems of the form "X is Y percent of Z" is a cornerstone of mathematical literacy. It transcends simple arithmetic and provides a foundation for success in various fields, from personal finance to advanced statistical analysis. By understanding the core concepts, mastering the formulas, and practicing with real-world examples, you can equip yourself with a valuable skill set that will enhance your problem-solving abilities and contribute to your overall success. The more you practice, the more intuitive these calculations will become, making them an effortless part of your daily life and professional endeavors. Remember to always check your work and consider the context of the problem to ensure your calculations are accurate and meaningful.
Latest Posts
Latest Posts
-
Find The Indicated Side Of The Triangle
May 09, 2025
-
How To Find A Scale Factor Of A Triangle
May 09, 2025
-
What Is The Lcm Of 3 And 11
May 09, 2025
-
30 Percent Off Of 35 Dollars
May 09, 2025
-
Cuantos Dias Faltan Para El 4 De Marzo
May 09, 2025
Related Post
Thank you for visiting our website which covers about X Is Y Percent Of Z . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.