0.2 Of What Number Is 8
Treneri
May 12, 2025 · 4 min read
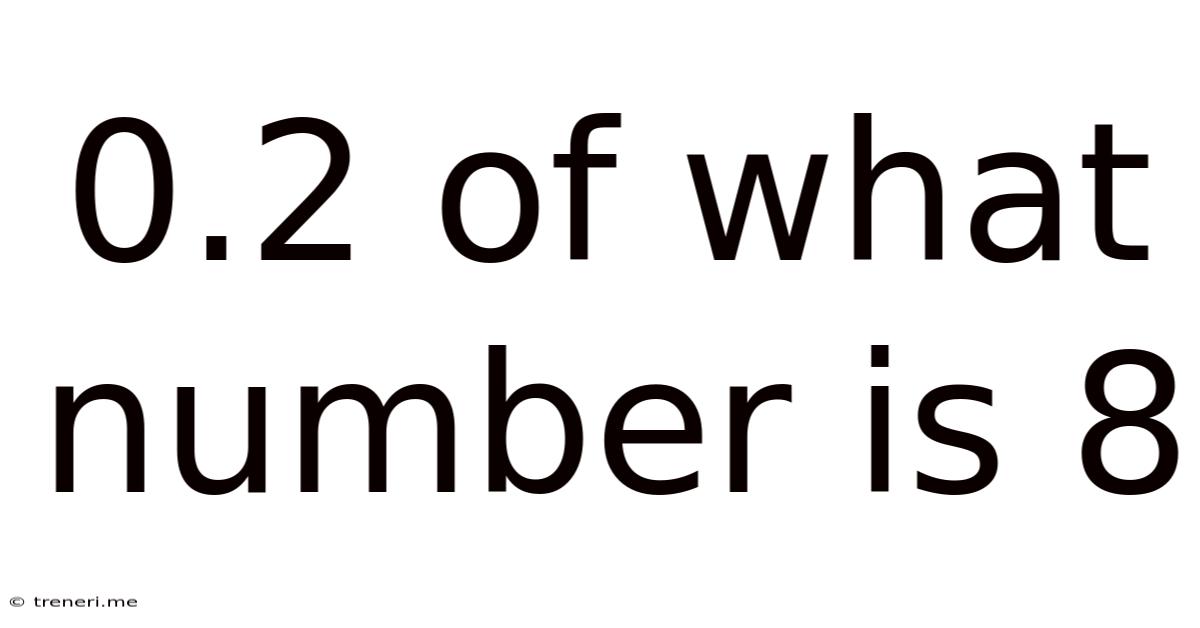
Table of Contents
0.2 of What Number is 8? Unraveling the Mystery of Percentage Calculations
Finding an unknown number based on a percentage can seem daunting, but with a structured approach, it becomes straightforward. This article delves deep into the problem "0.2 of what number is 8," explaining the solution methodically, providing variations of the problem, and exploring the broader concepts of percentages and their applications in real-world scenarios.
Understanding the Problem: Deconstructing "0.2 of What Number is 8?"
The question, "0.2 of what number is 8," essentially asks us to find a number (let's call it 'x') such that 20% (or 0.2 expressed as a decimal) of that number equals 8. This is a fundamental percentage problem solvable using algebraic equations.
Translating Words into an Equation
Let's break down the sentence into mathematical terms:
- "0.2 of" translates to 0.2 multiplied by (×)
- "what number" represents our unknown, which we denote as 'x'
- "is 8" translates to an equals sign (=) and the number 8
Therefore, the entire sentence becomes the equation: 0.2x = 8
Solving the Equation: Finding the Unknown Number
Now that we have an equation, we can solve for 'x' using basic algebra. The goal is to isolate 'x' on one side of the equation.
Step-by-Step Solution
-
Divide both sides by 0.2: To isolate 'x', we need to perform the inverse operation of multiplication, which is division. Dividing both sides of the equation by 0.2 gives us:
x = 8 / 0.2 -
Perform the division: Dividing 8 by 0.2 yields:
x = 40
Therefore, 0.2 of 40 is 8.
Verifying the Solution: Checking Your Answer
It's crucial to verify our solution to ensure accuracy. We can do this by substituting the value of 'x' (which is 40) back into the original equation:
0.2 * 40 = 8
Since the equation holds true, our solution (x = 40) is correct.
Alternative Approaches: Exploring Different Methods
While the algebraic approach is efficient, we can explore alternative methods to solve this type of problem, offering a deeper understanding of percentage calculations.
Method 1: Using Fractions
We can express 0.2 as a fraction: 0.2 = 1/5. The equation then becomes:
(1/5)x = 8
Multiplying both sides by 5 to isolate 'x':
x = 8 * 5
x = 40
This method reinforces the relationship between decimals and fractions, providing a different perspective on the problem.
Method 2: Percentage to Decimal Conversion
Understanding the conversion between percentages and decimals is fundamental. 0.2 is equivalent to 20%. The problem can be rephrased as: "20% of what number is 8?"
We can express 20% as a decimal (0.2) or a fraction (1/5), then proceed with the algebraic solution as shown above.
Real-World Applications: Percentage Problems in Everyday Life
Percentage calculations are ubiquitous in daily life. Understanding how to solve problems like "0.2 of what number is 8" is essential in various contexts:
- Sales and Discounts: Calculating the original price of an item after a 20% discount. If the discounted price is $8, the original price is found using the same method.
- Financial Calculations: Determining the principal amount of an investment that yielded a 20% return resulting in $8 profit.
- Scientific Measurements: Calculating the initial quantity of a substance after a 20% reduction.
- Data Analysis: Interpreting data represented as percentages. For example, if 20% of a survey group answered "yes," and that represents 8 respondents, the total number of respondents can be determined.
Variations and Extensions: Expanding the Problem
Let's explore variations of the problem to solidify understanding and tackle more complex scenarios:
Variation 1: Different Percentage
What if the problem were: "0.35 of what number is 14?" The method remains the same. We set up the equation: 0.35x = 14. Dividing both sides by 0.35 gives us x = 40.
Variation 2: Unknown Percentage
What if the problem were: "x% of 40 is 8?" Here, we need to solve for the percentage 'x'. The equation would be: (x/100) * 40 = 8. Solving for 'x' would show that x = 20%.
Variation 3: Larger Numbers and Decimals
Let's consider a problem with larger numbers and decimals: "0.075 of what number is 15?" This involves a more complex division but follows the same core principles of setting up an equation and solving for the unknown. The solution, using the same method, yields 200.
Mastering Percentage Calculations: Tips and Tricks
- Practice consistently: Solving a variety of percentage problems is key to mastering the concept.
- Understand the relationships: Grasp the connections between decimals, fractions, and percentages.
- Use different methods: Experiment with algebraic solutions, fraction methods, and other approaches to deepen your understanding.
- Check your work: Always verify your solution by substituting the value back into the original equation.
- Utilize online resources: Many online calculators and tutorials are available for additional practice and support.
Conclusion: Embracing the Power of Percentages
Understanding percentage calculations, including solving problems like "0.2 of what number is 8," is a valuable skill applicable across numerous fields. By mastering the fundamental techniques and applying them consistently, you can confidently tackle various percentage-related challenges in your daily life and professional endeavors. Remember that practice is key, and exploring different approaches will solidify your grasp of this crucial mathematical concept. From simple everyday transactions to complex scientific calculations, the ability to work with percentages is an invaluable asset.
Latest Posts
Latest Posts
-
7 Is What Percent Of 30
May 12, 2025
-
22 Km To Miles Per Hour
May 12, 2025
-
Cuantos Pies Cuadrados Es Una Yarda
May 12, 2025
-
Cuantos Dias Hay Desde El 10 De Junio Hasta Hoy
May 12, 2025
-
1 Cubic Foot Of Soil To Gallons
May 12, 2025
Related Post
Thank you for visiting our website which covers about 0.2 Of What Number Is 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.