7 Is What Percent Of 30
Treneri
May 12, 2025 · 5 min read
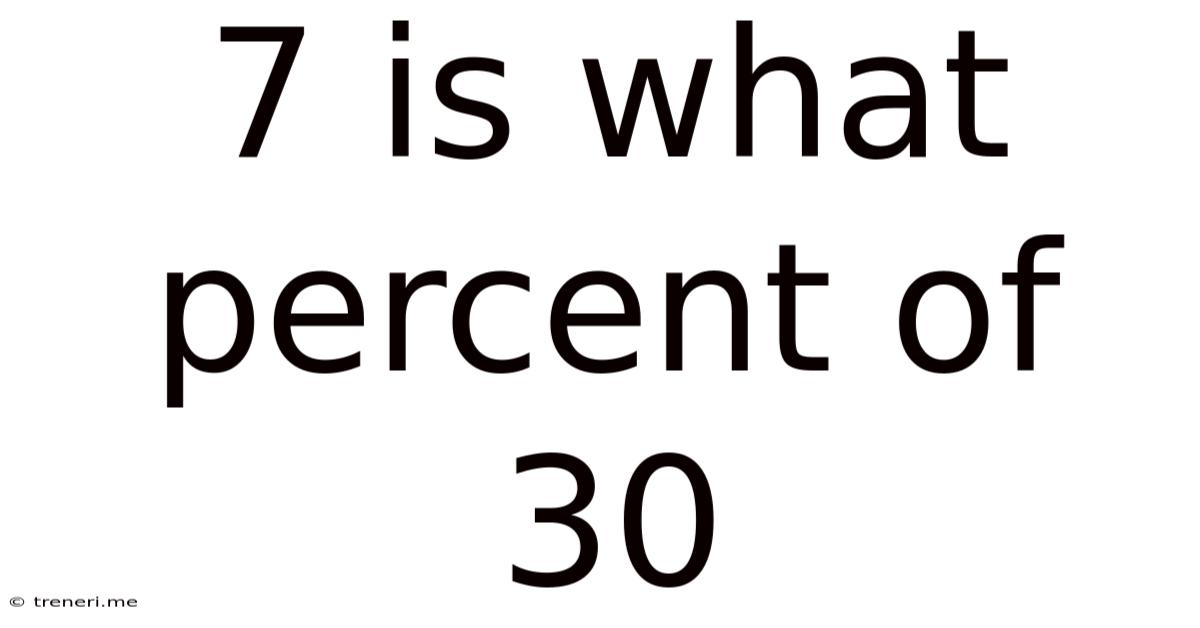
Table of Contents
7 is What Percent of 30? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill with widespread applications in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide delves into the question, "7 is what percent of 30?", providing not only the answer but also a thorough explanation of the underlying principles and different methods for solving percentage problems. We will explore various approaches, including the formula method, the proportion method, and the unitary method, equipping you with a versatile skill set to tackle similar percentage calculations with ease.
Understanding Percentages
A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" is used to denote percentages. Essentially, a percentage represents a portion of a whole. For instance, 50% means 50 out of 100, or one-half. Understanding this fundamental concept is key to solving percentage problems efficiently.
Calculating "7 is What Percent of 30?" – The Formula Method
The most straightforward method to determine what percentage 7 represents of 30 is using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 7
- Whole: 30
Plugging these values into the formula, we get:
(7 / 30) * 100% = 23.33% (approximately)
Therefore, 7 is approximately 23.33% of 30.
Understanding the Calculation
The formula essentially converts the fraction representing the part-to-whole relationship into a percentage by multiplying it by 100. Dividing 7 by 30 gives us the decimal representation of the fraction (0.2333...). Multiplying this decimal by 100 converts it into a percentage.
Calculating "7 is What Percent of 30?" – The Proportion Method
The proportion method offers an alternative approach to solving percentage problems. It involves setting up a proportion, equating two ratios:
Part / Whole = Percentage / 100
Using the given values:
7 / 30 = x / 100
To solve for 'x' (the percentage), we cross-multiply:
30x = 700
x = 700 / 30
x ≈ 23.33
Again, we arrive at the same result: 7 is approximately 23.33% of 30.
Advantages of the Proportion Method
The proportion method can be particularly helpful when dealing with more complex percentage problems or when you need to find the part or the whole given the percentage and one of the other values. It offers a structured approach to solving these types of problems.
Calculating "7 is What Percent of 30?" – The Unitary Method
The unitary method focuses on finding the value of one unit (1%) before calculating the required percentage. This is a particularly useful approach for beginners or for those working with simpler percentage calculations.
First, find the value of 1% of 30:
30 / 100 = 0.3
This means 1% of 30 is 0.3.
Now, multiply this value by 7 to find what 7 represents as a percentage of 30:
0.3 * 7 = 2.1
Then, divide 2.1 by 0.3 to find the percentage:
2.1 / 0.3 = 7
This may seem confusing in this specific example because the resulting number is not a percentage, but rather a multiple of 0.3. The critical step was missed; after getting 2.1, you should multiply by 100 to determine the percentage. Thus, 2.1 * 100 = 210%. This shows a flaw in this method's applicability to this particular question. The unitary method is more effective when you need to find a percentage of a given number, rather than determining what percentage one number is of another.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios:
- Financial Calculations: Calculating interest rates, discounts, taxes, profit margins, and tips.
- Data Analysis: Interpreting statistical data, analyzing survey results, and understanding market trends.
- Scientific Applications: Expressing concentrations, calculating experimental results, and representing proportions.
- Everyday Life: Comparing prices, understanding sale offers, and calculating proportions in recipes.
Advanced Percentage Problems and Their Solutions
While the problem "7 is what percent of 30?" is relatively straightforward, let's explore some more advanced percentage scenarios and how to approach them.
Scenario 1: Finding the Whole
Let's say you know that 15% of a number is 6. What is the number?
We can use the formula:
(Part / Whole) * 100% = Percentage
Substitute the known values:
(6 / Whole) * 100% = 15%
Solving for "Whole":
Whole = (6 / 15) * 100 = 40
Therefore, the number is 40.
Scenario 2: Finding the Percentage Increase or Decrease
If a price increases from $20 to $25, what is the percentage increase?
First, calculate the difference: $25 - $20 = $5
Then, divide the difference by the original price and multiply by 100%:
(5 / 20) * 100% = 25%
The price increased by 25%.
Scenario 3: Compound Percentage Changes
Suppose a value increases by 10% and then decreases by 10%. Is the final value the same as the original?
No. Let's illustrate with an example:
Original value: $100
Increase by 10%: $100 * 1.10 = $110
Decrease by 10%: $110 * 0.90 = $99
The final value is $99, which is less than the original value. This demonstrates the non-linear nature of compound percentage changes.
Mastering Percentage Calculations: Tips and Tricks
- Practice regularly: The more you practice, the more comfortable you'll become with solving percentage problems.
- Use different methods: Experiment with the formula method, the proportion method, and the unitary method to find the approach that suits you best.
- Check your answers: Always double-check your calculations to ensure accuracy.
- Break down complex problems: Divide complex problems into smaller, more manageable steps.
- Utilize online resources: Numerous websites and apps offer percentage calculators and practice problems.
Conclusion: Beyond the Basics of Percentages
This comprehensive guide has not only answered the question, "7 is what percent of 30?" but also provided a solid foundation for understanding and applying percentage calculations in various contexts. By mastering these techniques, you'll be equipped to confidently tackle percentage problems in your academic pursuits, professional life, and everyday decision-making. Remember to practice consistently and explore different approaches to solidify your understanding and enhance your problem-solving skills. The ability to work with percentages is a valuable asset, and with dedicated practice, it's a skill easily mastered.
Latest Posts
Latest Posts
-
How Many Minutes Is 80 Seconds
May 12, 2025
-
Moment Of Inertia Of A Tube
May 12, 2025
-
2 7 1 4 As A Fraction
May 12, 2025
-
Cuanto Es 11 81 Pulgadas En Centimetros
May 12, 2025
-
How Many Tablespoons Is 12 Cloves Of Garlic
May 12, 2025
Related Post
Thank you for visiting our website which covers about 7 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.