1 1 1 1 In Binary
Treneri
May 10, 2025 · 6 min read
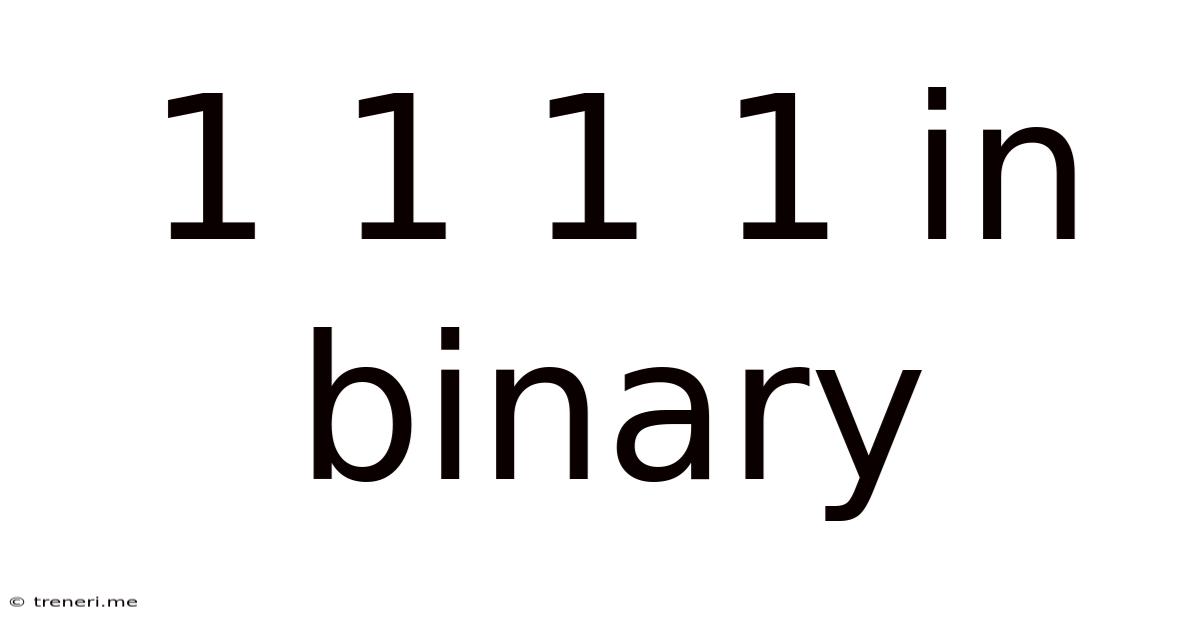
Table of Contents
Decoding the Mystery: A Deep Dive into 1 1 1 1 in Binary
The seemingly simple sequence "1 1 1 1" in binary holds a surprising depth of meaning and application within the world of computer science and digital systems. While at first glance it might appear rudimentary, understanding its implications unlocks a gateway to comprehending fundamental concepts like binary representation, bit manipulation, and their broader applications in various fields. This article will explore this seemingly simple sequence, examining its different interpretations, practical applications, and the underlying principles that govern its significance.
Understanding Binary Representation: The Foundation of 1 1 1 1
Before delving into the specifics of "1 1 1 1", it's crucial to establish a foundational understanding of the binary number system. Unlike the decimal system we use daily (base-10, using digits 0-9), the binary system is a base-2 system, employing only two digits: 0 and 1. These digits, known as bits (binary digits), are the fundamental building blocks of all digital information.
Each position in a binary number represents a power of 2. Starting from the rightmost position (least significant bit), the positions represent 2⁰, 2¹, 2², 2³, and so on. Therefore, the binary number 1011 translates to:
(1 * 2³) + (0 * 2²) + (1 * 2¹) + (1 * 2⁰) = 8 + 0 + 2 + 1 = 11 (in decimal)
This simple conversion highlights the core principle: binary uses powers of 2 to represent numerical values.
Interpreting "1 1 1 1" in Binary: Different Perspectives
The sequence "1 1 1 1" can be interpreted in several ways, depending on the context:
1. As a Binary Number:
If we treat "1 1 1 1" as a single binary number, its decimal equivalent is straightforward to calculate:
(1 * 2³) + (1 * 2²) + (1 * 2¹) + (1 * 2⁰) = 8 + 4 + 2 + 1 = 15
Therefore, "1 1 1 1" in binary represents the decimal number 15. This simple representation forms the basis for more complex computations and data storage within digital systems.
2. As Individual Bits:
Considering each "1" as an independent bit opens up possibilities for its application in various digital operations. Each bit can represent a distinct piece of information, a flag indicating a specific state, or a component of a larger data structure. For example:
- Flags: In programming, a single bit can act as a flag, representing a true/false condition (1 for true, 0 for false). Four bits (like "1 1 1 1") could represent four independent flags controlling different aspects of a system.
- Bitmasks: Bitmasks are used for selective operations on data. The sequence "1 1 1 1" as a bitmask could be used to "mask" (select) all four bits of a larger binary number.
- Data Encoding: Each "1" might be part of a larger encoding scheme representing characters, colors, or other types of data.
3. As a Nibble:
In computer architecture, a nibble (or nybble) is a four-bit unit of data. Therefore, "1 1 1 1" perfectly represents a single nibble. Nibbles are frequently used as building blocks in larger data structures and play a significant role in data compression and efficient storage. They are a fundamental component in hexadecimal representation, where each hexadecimal digit corresponds to a nibble.
Applications of "1 1 1 1" in Binary: Real-world Examples
The seemingly insignificant sequence "1 1 1 1" finds practical applications in various domains:
1. Computer Programming:
- Bit manipulation: Programmers manipulate individual bits to perform operations like setting flags, clearing bits, or testing bit values. The sequence "1 1 1 1" is a simple example, and understanding its behavior is key to mastering bitwise operations in various programming languages (C, C++, Java, Python, etc.).
- Data Structures: Data structures like arrays and bit fields heavily rely on the organization and manipulation of individual bits. Understanding binary representation is fundamental for effectively managing these data structures.
- Logical Operations: Bitwise logical operations (AND, OR, XOR, NOT) utilize binary sequences to perform calculations at a low level. "1 1 1 1" can serve as an operand in these operations, determining the final result.
2. Digital Electronics:
- Logic Gates: Digital circuits utilize logic gates (AND, OR, NOT, XOR) that operate on binary inputs. The "1 1 1 1" sequence can represent input signals to these gates, affecting the output.
- Microcontrollers: Microcontrollers commonly use binary representations for internal registers and memory addresses. Understanding the implications of binary sequences is critical for programming and interacting with microcontrollers.
- Digital Signal Processing (DSP): DSP systems extensively rely on binary signals and operations. The representation and manipulation of binary data, including sequences like "1 1 1 1," are central to implementing DSP algorithms.
3. Networking and Communications:
- IP Addresses: While IP addresses are typically represented in decimal dotted notation, their underlying representation is binary. Understanding binary is crucial for network engineers and programmers working with IP addresses, subnets, and other network parameters.
- Data Transmission: Data transmitted over networks is ultimately represented as sequences of bits (0s and 1s). Analyzing and interpreting these sequences is vital for network communication protocols.
- Error Detection and Correction: Numerous error detection and correction codes utilize binary representations to ensure reliable data transmission.
Extending the Concept: Beyond "1 1 1 1"
While "1 1 1 1" provides a simple example, understanding the principles of binary representation extends to more complex scenarios. Larger binary numbers, binary arithmetic, and the relationship between binary and other number systems (decimal, hexadecimal, octal) are all crucial aspects of computer science and digital systems.
Hexadecimal Representation:
Hexadecimal (base-16) is a more concise way to represent binary data. Each hexadecimal digit represents four bits (a nibble). The binary sequence "1 1 1 1" is equivalent to the hexadecimal digit "F". This shorthand simplifies the representation of large binary numbers.
Binary Arithmetic:
Binary arithmetic involves performing mathematical operations (addition, subtraction, multiplication, division) directly on binary numbers. Understanding binary arithmetic is fundamental for digital circuit design and programming low-level operations.
Beyond Numbers: Representing Data
Binary isn't just about numbers. It's the foundation for representing all forms of digital data: text, images, audio, and video. Each type of data has its own encoding scheme that converts it into a binary format for storage and processing.
Conclusion: The Enduring Significance of Binary
The seemingly simple sequence "1 1 1 1" in binary serves as a microcosm of the fundamental principles governing the digital world. Its various interpretations, from a simple decimal number to a crucial component in data structures and algorithms, highlight its significance. Understanding its implications unlocks a deeper comprehension of computer science, digital electronics, and the vast array of technologies built upon the binary foundation. Mastering binary is not just a technical skill; it's the key to unlocking the inner workings of the digital age and its ever-evolving landscape. From the simplest microcontrollers to the most powerful supercomputers, the language of "1" and "0" remains the cornerstone of our technological world. The seemingly simple "1 1 1 1" truly represents the power and versatility of binary code.
Latest Posts
Latest Posts
-
What Should Salt Ppm Be For Pool
May 10, 2025
-
249 Rounded To The Nearest Hundred
May 10, 2025
-
What Day Was It 120 Days Ago
May 10, 2025
-
21 Is What Percent Of 20
May 10, 2025
-
Find The Volume Of The Following Figure
May 10, 2025
Related Post
Thank you for visiting our website which covers about 1 1 1 1 In Binary . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.