1/2 + 1/8 In Fraction Form
Treneri
May 11, 2025 · 6 min read
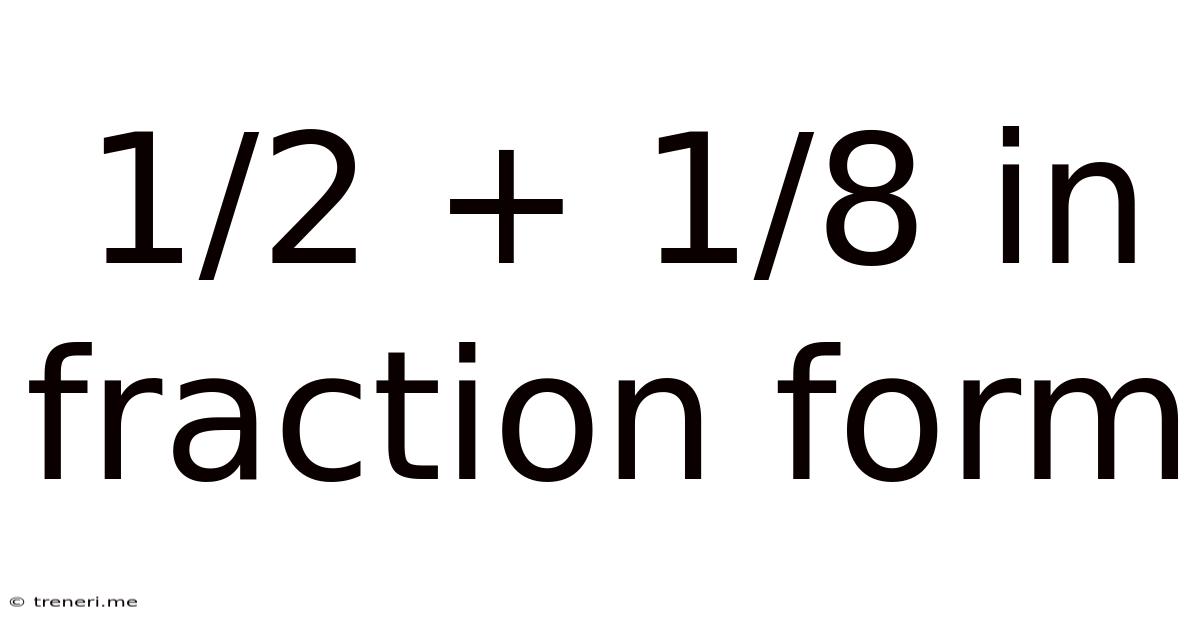
Table of Contents
1/2 + 1/8: A Deep Dive into Fraction Addition
Adding fractions might seem like a simple arithmetic task, but understanding the underlying principles and mastering the techniques is crucial for a strong foundation in mathematics. This comprehensive guide will explore the addition of 1/2 and 1/8, covering various aspects, including finding the least common denominator (LCD), simplifying fractions, and real-world applications. We'll also delve into the broader context of fraction addition, providing you with a robust understanding you can apply to more complex problems.
Understanding Fractions: A Quick Refresher
Before we tackle the addition of 1/2 and 1/8, let's briefly revisit the fundamental concepts of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator is 1 (we have one part), and the denominator is 2 (the whole is divided into two equal parts).
Finding the Least Common Denominator (LCD)
Adding fractions with different denominators requires finding a common denominator – a number that is a multiple of both denominators. The most efficient approach is to find the least common denominator (LCD). This simplifies the calculations and results in a fraction that is already in its simplest form.
To find the LCD of 2 and 8:
-
List the multiples of each denominator:
- Multiples of 2: 2, 4, 6, 8, 10, 12...
- Multiples of 8: 8, 16, 24...
-
Identify the smallest common multiple: The smallest number appearing in both lists is 8. Therefore, the LCD of 2 and 8 is 8.
Adding the Fractions: 1/2 + 1/8
Now that we've found the LCD, we can proceed with the addition:
-
Convert the fractions to equivalent fractions with the LCD:
-
1/2 needs to be converted to an equivalent fraction with a denominator of 8. To do this, we multiply both the numerator and the denominator by 4: (1 * 4) / (2 * 4) = 4/8
-
1/8 already has a denominator of 8, so it remains unchanged.
-
-
Add the numerators: Now that both fractions have the same denominator, we can simply add their numerators:
4/8 + 1/8 = (4 + 1) / 8 = 5/8
Therefore, 1/2 + 1/8 = 5/8.
Simplifying Fractions
After adding fractions, it's essential to simplify the result to its lowest terms. A fraction is in its simplest form when the greatest common divisor (GCD) of the numerator and denominator is 1. In our case, 5/8 is already in its simplest form because the GCD of 5 and 8 is 1. There are no common factors other than 1.
Visual Representation: Understanding Fraction Addition Geometrically
Let's visualize the addition of 1/2 and 1/8 using a geometric representation. Imagine a circle divided into 8 equal slices (representing the denominator 8).
- 1/2: This represents 4 out of the 8 slices (4/8).
- 1/8: This represents 1 out of the 8 slices (1/8).
Adding 1/2 (4/8) and 1/8 together means combining 4 slices and 1 slice, resulting in a total of 5 slices out of 8. This visually confirms that 1/2 + 1/8 = 5/8.
Real-World Applications: Where Fraction Addition Matters
Fraction addition is not just an abstract mathematical concept; it finds practical application in numerous real-world scenarios:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Adding fractions accurately ensures the correct proportions are maintained. For example, a recipe might call for 1/2 cup of flour and 1/8 cup of sugar. Knowing how to add these fractions is crucial for successful baking.
-
Construction and Engineering: Precise measurements are paramount in construction and engineering projects. Fractions are used extensively in blueprints and calculations, and accurate addition is vital to ensuring structural integrity and functionality.
-
Finance: Fractions are used to represent portions of investments, shares, and debts. Adding fractions helps in calculating overall financial positions and understanding profit/loss scenarios.
-
Time Management: We often encounter fractional representations of time (e.g., 1/2 hour, 1/4 hour). Adding these fractional units is essential for accurate time planning and scheduling.
Extending the Concept: Adding More Than Two Fractions
The principles discussed above can be extended to adding more than two fractions. The key steps remain the same:
- Find the LCD: Determine the least common denominator for all fractions involved.
- Convert to Equivalent Fractions: Convert each fraction to an equivalent fraction with the LCD as the denominator.
- Add the Numerators: Add the numerators of the equivalent fractions.
- Simplify: Simplify the resulting fraction to its lowest terms.
Example: 1/2 + 1/4 + 1/8
- LCD: The LCD of 2, 4, and 8 is 8.
- Equivalent Fractions: 1/2 = 4/8; 1/4 = 2/8; 1/8 = 1/8
- Addition: 4/8 + 2/8 + 1/8 = 7/8
- Simplification: 7/8 is already in its simplest form.
Subtracting Fractions: A Related Concept
While this article focuses on addition, it's important to note that the principles of finding the LCD and converting to equivalent fractions are also crucial for subtracting fractions. The process is similar, except you subtract the numerators instead of adding them.
Mastering Fractions: A Building Block for Mathematical Proficiency
A strong understanding of fractions, including addition, is a fundamental building block for success in higher-level mathematics. From algebra and calculus to more advanced subjects, the ability to manipulate and work with fractions confidently is essential. The more you practice, the more comfortable and proficient you'll become. Regular practice with various fraction problems, incorporating both simple and complex scenarios, will solidify your understanding and build your confidence. Remember to always check your work, ensuring your answers are simplified and accurate. By mastering fractions, you're equipping yourself with a vital skillset that extends far beyond the classroom.
Troubleshooting Common Mistakes
Even experienced mathematicians occasionally stumble when working with fractions. Here are some common mistakes to watch out for:
- Forgetting to find the LCD: Adding fractions with different denominators without finding the LCD will lead to incorrect answers.
- Incorrectly converting to equivalent fractions: Ensure you multiply both the numerator and the denominator by the same number when converting fractions.
- Adding or subtracting denominators: Remember that you only add or subtract the numerators; the denominator remains the same after the operation.
- Failing to simplify: Always simplify your answer to its lowest terms.
By being mindful of these common pitfalls, you can improve your accuracy and efficiency when working with fractions.
Conclusion: Embrace the Power of Fractions
Fractions, though seemingly simple, are powerful mathematical tools that underpin numerous real-world applications. Mastering the fundamentals of fraction addition, including finding the LCD and simplifying fractions, is crucial for both academic success and practical problem-solving. Through practice and understanding, you can confidently navigate the world of fractions and leverage their power in various aspects of your life. Remember to break down complex problems into smaller, manageable steps, and always double-check your work. With consistent effort, you will develop a robust understanding of fractions and their importance in mathematical computation and real-world scenarios.
Latest Posts
Latest Posts
-
Find The Area Of The Following Shape
May 12, 2025
-
17 Divided By 3 With Remainder
May 12, 2025
-
13 Out Of 18 As A Grade
May 12, 2025
-
What Is The Percentage Of 12 Out Of 16
May 12, 2025
-
5 3 4 As A Fraction
May 12, 2025
Related Post
Thank you for visiting our website which covers about 1/2 + 1/8 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.