1 3 Divided By 3 4 As A Fraction
Treneri
May 12, 2025 · 5 min read
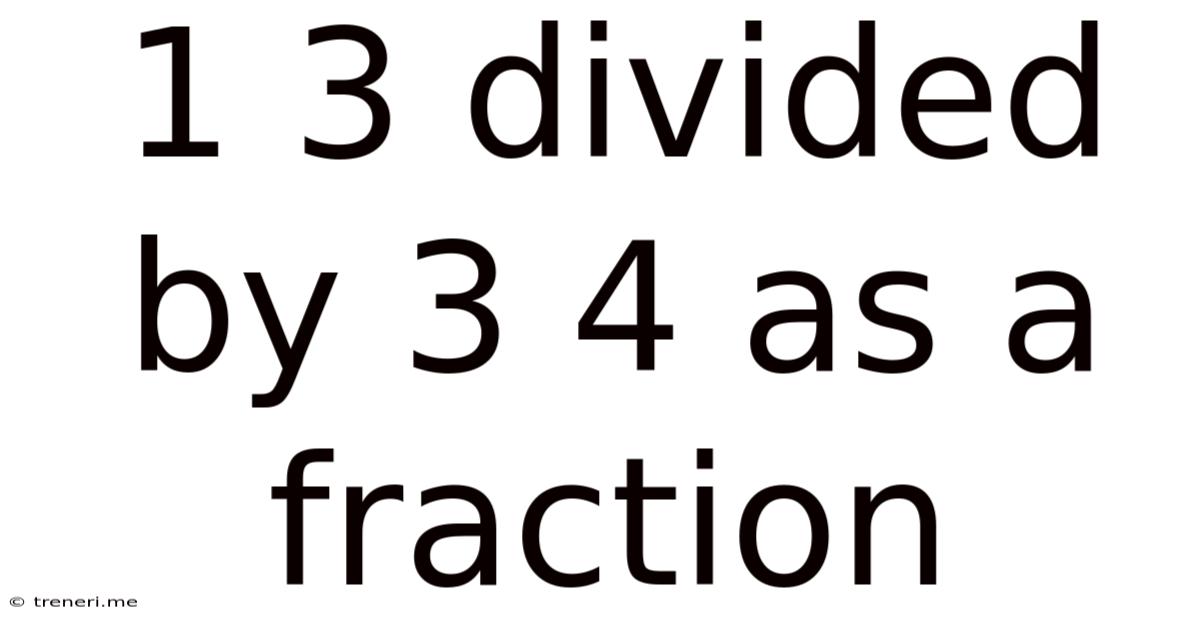
Table of Contents
1 3/4 Divided by 3/4: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting, especially when mixed numbers are involved. But with a clear understanding of the process, even complex fraction divisions, like 1 3/4 divided by 3/4, become manageable and even straightforward. This comprehensive guide will walk you through the steps, explaining the concepts and providing practical examples to solidify your understanding. We'll explore multiple approaches, ensuring you can tackle similar problems with confidence.
Understanding Fractions and Mixed Numbers
Before diving into the division, let's refresh our understanding of fractions and mixed numbers.
Fractions: The Building Blocks
A fraction represents a part of a whole. It's composed of two parts:
- Numerator: The top number, indicating how many parts you have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, the numerator is 3 (you have 3 parts), and the denominator is 4 (the whole is divided into 4 equal parts).
Mixed Numbers: Combining Whole and Fractional Parts
A mixed number combines a whole number and a fraction. For instance, 1 3/4 represents one whole unit and three-quarters of another. Understanding how to convert between mixed numbers and improper fractions is crucial for fraction division.
Converting Mixed Numbers to Improper Fractions
To divide fractions effectively, it's generally easier to work with improper fractions. An improper fraction is a fraction where the numerator is greater than or equal to the denominator. Here's how to convert a mixed number to an improper fraction:
- Multiply the whole number by the denominator: In our example, 1 3/4, we multiply 1 (the whole number) by 4 (the denominator) which equals 4.
- Add the numerator: Add the result from step 1 to the numerator of the fraction (3 in our case): 4 + 3 = 7.
- Keep the same denominator: The denominator remains 4.
Therefore, 1 3/4 is equal to the improper fraction 7/4.
The Reciprocal: The Key to Fraction Division
The reciprocal of a fraction is simply the fraction flipped upside down. To find the reciprocal, switch the numerator and the denominator. For example, the reciprocal of 3/4 is 4/3. The reciprocal is the key to dividing fractions.
Dividing Fractions: The "Keep, Change, Flip" Method
The most common and easiest method for dividing fractions is the "Keep, Change, Flip" method. Let's apply this method to our problem: 1 3/4 divided by 3/4.
- Keep: Keep the first fraction (after converting it to an improper fraction). We've already converted 1 3/4 to 7/4, so we keep 7/4.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip (find the reciprocal of) the second fraction. The reciprocal of 3/4 is 4/3.
This transforms our problem from 7/4 ÷ 3/4 to 7/4 × 4/3.
Multiplying Fractions: A Simpler Operation
Multiplying fractions is much simpler than dividing them. To multiply fractions:
- Multiply the numerators: 7 × 4 = 28
- Multiply the denominators: 4 × 3 = 12
This gives us the fraction 28/12.
Simplifying Fractions: Reducing to Lowest Terms
The fraction 28/12 is not in its simplest form. To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator and divide both by it. The GCD of 28 and 12 is 4.
Dividing both the numerator and denominator by 4, we get:
28 ÷ 4 = 7 12 ÷ 4 = 3
Therefore, the simplified fraction is 7/3.
Converting Improper Fractions to Mixed Numbers
The result 7/3 is an improper fraction. To convert it back to a mixed number:
- Divide the numerator by the denominator: 7 ÷ 3 = 2 with a remainder of 1.
- The quotient becomes the whole number: The quotient (2) is the whole number part of the mixed number.
- The remainder becomes the numerator: The remainder (1) is the numerator of the fraction.
- Keep the same denominator: The denominator remains 3.
Therefore, 7/3 is equal to 2 1/3.
Solution: 1 3/4 divided by 3/4 = 2 1/3
Following these steps, we have successfully solved the problem: 1 3/4 divided by 3/4 equals 2 1/3.
Alternative Methods: Visualizing Fraction Division
While the "Keep, Change, Flip" method is efficient, visualizing fraction division can enhance understanding. Consider using diagrams or models to represent the fractions. Imagine dividing a pizza cut into four slices (representing 3/4) into portions of 1 and 3/4 slices. This visual representation will reinforce the concept.
Real-World Applications of Fraction Division
Understanding fraction division is vital in various real-world situations, including:
- Cooking and Baking: Scaling recipes up or down requires accurate fraction division.
- Sewing and Crafting: Calculating fabric or material quantities often involves fractions.
- Construction and Engineering: Precise measurements in building and engineering projects require understanding fraction division.
- Finance and Budgeting: Dividing resources and allocating funds necessitates working with fractions.
Practicing Fraction Division: Tips and Tricks
Mastering fraction division requires consistent practice. Here are some tips to improve your skills:
- Start with simpler problems: Begin with easier fraction divisions before tackling more complex ones.
- Use visual aids: Diagrams and models can make the process clearer.
- Break down complex problems: Divide the problem into smaller, manageable steps.
- Check your work: Always verify your answer by performing the reverse operation (multiplication).
- Practice regularly: Consistent practice is key to improving your proficiency.
Advanced Concepts: Dividing Fractions with Variables
The principles of fraction division extend to algebraic expressions involving variables. The same "Keep, Change, Flip" method applies, with variables treated as numerical values. For example, (x/y) ÷ (a/b) becomes (x/y) × (b/a) = xb/ya.
Conclusion: Mastering Fraction Division for Success
Fraction division, even with mixed numbers, is a fundamental skill with broad applications. By understanding the underlying concepts, utilizing the "Keep, Change, Flip" method, and practicing regularly, you can confidently tackle any fraction division problem and enhance your mathematical proficiency. Remember that consistent practice and a clear grasp of the core principles are the keys to mastering this essential skill. This deep understanding will prove invaluable in various academic and real-world scenarios. The seemingly complex calculation of 1 3/4 divided by 3/4 is now a solvable puzzle, a testament to the power of breaking down challenging problems into smaller, more manageable steps.
Latest Posts
Latest Posts
-
650 Board Feet To Square Feet
May 14, 2025
-
What Is The Square Root Of 62
May 14, 2025
-
1 2 Divided By 2 3 In Fraction Form
May 14, 2025
-
4 And 7 8 As An Improper Fraction
May 14, 2025
-
How Many Cubic Feet In 40 Pounds
May 14, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Divided By 3 4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.