1/6 + 1/10 In Simplest Form
Treneri
May 14, 2025 · 5 min read
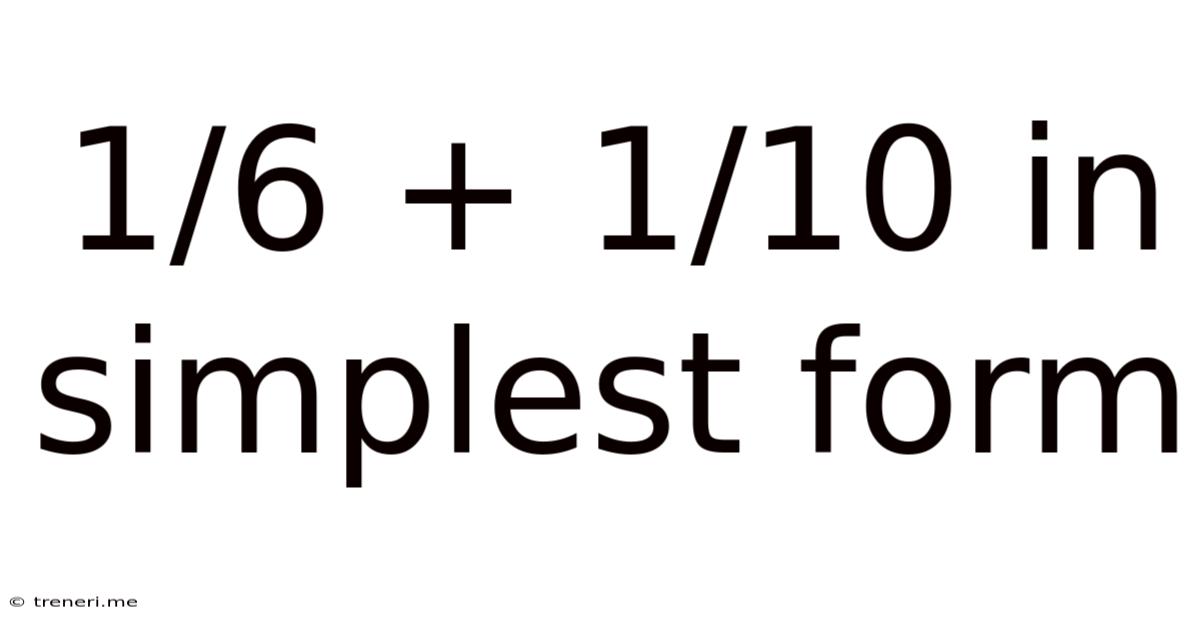
Table of Contents
1/6 + 1/10 in Simplest Form: A Comprehensive Guide to Fraction Addition
Adding fractions might seem like a simple arithmetic task, but understanding the underlying principles and mastering the techniques is crucial for a strong foundation in mathematics. This comprehensive guide will delve into the process of adding 1/6 and 1/10, explaining the steps involved, exploring related concepts, and offering practical applications. We'll cover everything from finding the least common denominator (LCD) to simplifying the final answer and even touch upon the broader implications of fraction addition in various fields.
Understanding Fractions: A Quick Recap
Before we jump into adding 1/6 and 1/10, let's quickly review the fundamentals of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating the number of parts considered.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/6, the numerator is 1 (representing one part) and the denominator is 6 (representing six equal parts).
Finding the Least Common Denominator (LCD)
Adding fractions with different denominators requires finding a common denominator – a number that is divisible by both denominators. The most efficient approach is to find the least common denominator (LCD). This simplifies the calculation and results in the simplest form of the answer.
To find the LCD of 6 and 10, we can use several methods:
Method 1: Listing Multiples
List the multiples of each denominator:
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 10: 10, 20, 30, 40, 50...
The smallest number appearing in both lists is 30. Therefore, the LCD of 6 and 10 is 30.
Method 2: Prime Factorization
This method is particularly useful for larger denominators. Find the prime factorization of each denominator:
- 6 = 2 x 3
- 10 = 2 x 5
The LCD is found by taking the highest power of each prime factor present in either factorization: 2 x 3 x 5 = 30.
Adding the Fractions
Now that we have the LCD (30), we can rewrite the fractions with this common denominator:
- 1/6 = (1 x 5) / (6 x 5) = 5/30 (We multiplied both the numerator and denominator by 5)
- 1/10 = (1 x 3) / (10 x 3) = 3/30 (We multiplied both the numerator and denominator by 3)
Now we can add the fractions:
5/30 + 3/30 = (5 + 3) / 30 = 8/30
Simplifying the Fraction
The fraction 8/30 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of the numerator (8) and the denominator (30) and divide both by it.
The factors of 8 are 1, 2, 4, and 8. The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
The greatest common divisor of 8 and 30 is 2.
Dividing both the numerator and denominator by 2:
8/30 = (8 ÷ 2) / (30 ÷ 2) = 4/15
Therefore, the simplest form of 1/6 + 1/10 is 4/15.
Visualizing Fraction Addition
Understanding fraction addition can be enhanced through visualization. Imagine you have a pizza cut into 30 slices. 1/6 of the pizza represents 5 slices (30/6 = 5), and 1/10 represents 3 slices (30/10 = 3). Adding these together (5 slices + 3 slices = 8 slices) gives you 8/30 of the pizza, which simplifies to 4/15.
Practical Applications of Fraction Addition
Fraction addition isn't just an abstract mathematical concept; it has numerous real-world applications:
- Baking and Cooking: Following recipes often involves adding fractional amounts of ingredients. For example, combining 1/6 cup of sugar with 1/10 cup of flour requires adding fractions.
- Construction and Engineering: Precise measurements are critical in these fields, and fractions are frequently used in calculations involving lengths, volumes, and areas.
- Finance: Calculating percentages and proportions in financial analysis often necessitates fraction addition.
- Data Analysis: When dealing with proportions or percentages in data analysis, adding fractions is essential.
Further Exploration of Fraction Operations
Beyond addition, understanding other fraction operations – subtraction, multiplication, and division – is equally important. These operations build upon the same fundamental principles of numerators, denominators, and finding common denominators (or simplifying fractions when multiplying and dividing).
Subtracting Fractions
Subtracting fractions follows a similar process to addition. Find the LCD, rewrite the fractions with the common denominator, and then subtract the numerators. For example, subtracting 1/10 from 1/6 would be:
1/6 - 1/10 = 5/30 - 3/30 = 2/30 = 1/15
Multiplying Fractions
Multiplying fractions is simpler than addition or subtraction. Simply multiply the numerators together and the denominators together. For example:
1/6 x 1/10 = (1 x 1) / (6 x 10) = 1/60
Dividing Fractions
Dividing fractions involves inverting (flipping) the second fraction and then multiplying. For example:
1/6 ÷ 1/10 = 1/6 x 10/1 = 10/6 = 5/3
Conclusion: Mastering Fraction Addition and Beyond
Adding 1/6 and 1/10, resulting in the simplified fraction 4/15, is a foundational step in understanding fraction arithmetic. This seemingly simple calculation opens the door to a deeper comprehension of fractions and their numerous applications in various aspects of life. Mastering fraction addition, along with other fraction operations, is crucial for success in mathematics and related fields. By understanding the underlying principles and practicing these techniques, you'll build a strong mathematical foundation that will serve you well in your academic and professional pursuits. Remember to always simplify your answer to its lowest terms for the most accurate and efficient result. The ability to confidently work with fractions is a valuable skill that extends far beyond the classroom.
Latest Posts
Latest Posts
-
What Fractions Are Equivalent To 2 5
May 14, 2025
-
90 Days From October 5 2023
May 14, 2025
-
Cuanto Falta Para El 27 De Diciembre
May 14, 2025
-
Cuanto Es 2 Grados Fahrenheit En Centigrados
May 14, 2025
-
How To Calculate Binding For A Quilt
May 14, 2025
Related Post
Thank you for visiting our website which covers about 1/6 + 1/10 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.