1 Is What Percent Of 30
Treneri
May 10, 2025 · 4 min read
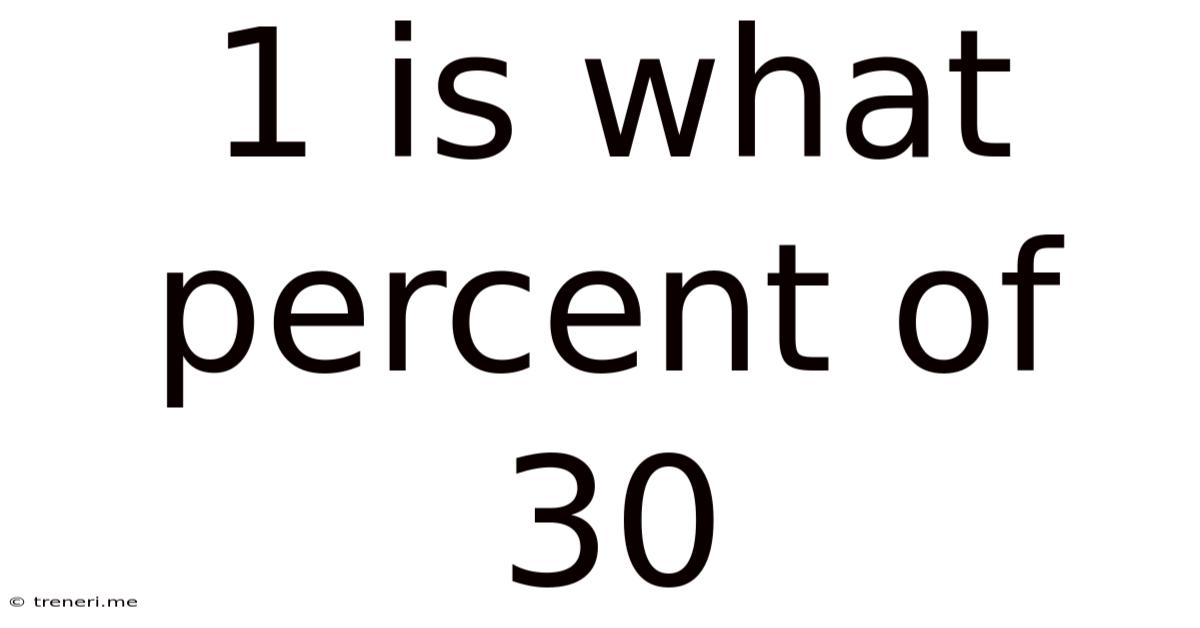
Table of Contents
1 is What Percent of 30? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and understanding statistics. This comprehensive guide delves into the question, "1 is what percent of 30?", providing not only the answer but also a thorough explanation of the underlying principles and various methods for solving similar percentage problems. We'll explore different approaches, discuss common mistakes to avoid, and equip you with the knowledge to confidently tackle any percentage calculation.
Understanding the Fundamentals of Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent" and signifies a portion of a whole. For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5. Percentages are a convenient way to express proportions and comparisons.
Method 1: Using the Percentage Formula
The most straightforward approach to determine what percentage 1 represents of 30 is by using the basic percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 1 (the value we want to express as a percentage)
- Whole: 30 (the total value)
Substituting these values into the formula:
(1 / 30) * 100% = 3.333...%
Therefore, 1 is approximately 3.33% of 30.
Method 2: Setting up a Proportion
Another effective method is to set up a proportion. A proportion is an equation stating that two ratios are equal. We can express the problem as:
1/30 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we can cross-multiply:
30x = 100
x = 100/30
x ≈ 3.33%
This method confirms the result obtained using the percentage formula.
Method 3: Using Decimal Conversion
We can also solve this by first converting the fraction 1/30 into a decimal:
1/30 ≈ 0.0333
Then, to convert this decimal to a percentage, we multiply by 100%:
0.0333 * 100% ≈ 3.33%
Practical Applications and Real-World Examples
Understanding percentage calculations is crucial in numerous real-life scenarios. Let's explore some examples:
Retail Discounts
Imagine a store offering a discount of 3.33% on an item originally priced at $30. The discount amount would be:
$30 * 0.0333 ≈ $1
This means the customer would save approximately $1.
Grade Calculations
If a student scores 1 point out of a possible 30 points on a test, their percentage score would be approximately 3.33%.
Financial Analysis
In finance, percentages are used extensively. For instance, calculating return on investment (ROI) often involves percentage calculations. If an investment of $30 yielded a profit of $1, the ROI would be approximately 3.33%.
Data Analysis and Statistics
Percentages are vital for interpreting data and drawing meaningful conclusions. For example, if 1 out of 30 participants in a survey responded positively to a particular question, the percentage of positive responses would be about 3.33%.
Common Mistakes to Avoid
While percentage calculations are relatively straightforward, several common mistakes can lead to inaccurate results:
-
Incorrect Formula Application: Using the wrong formula or incorrectly substituting values is a frequent error. Always double-check your formula and the values you're using.
-
Decimal Errors: Rounding off decimals prematurely can lead to inaccuracies. It's advisable to carry out calculations using the full decimal value until the final answer is obtained.
-
Percentage vs. Decimal Confusion: Remember to convert decimals to percentages (multiply by 100%) and vice versa (divide by 100%) when needed.
-
Mixing up Part and Whole: Ensure that you correctly identify the 'part' and 'whole' in the problem statement. The 'part' is the value you want to express as a percentage of the 'whole'.
Advanced Percentage Calculations
While the problem "1 is what percent of 30?" is relatively simple, understanding the underlying principles allows you to tackle more complex percentage problems. These include:
-
Calculating percentage increase or decrease: Determining the percentage change between two values.
-
Finding the original value after a percentage change: Working backward from a given percentage change to find the initial value.
-
Solving problems involving multiple percentages: Calculations involving consecutive percentage changes or discounts.
-
Applying percentages to compound interest calculations: Understanding how interest accumulates over time.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is essential for success in various fields. By understanding the fundamental formula, different solution methods, and common errors to avoid, you can confidently tackle any percentage problem. Remember to practice regularly and apply these concepts to real-world scenarios to solidify your understanding and improve your problem-solving skills. Whether it's calculating discounts, analyzing data, or understanding financial statements, a strong grasp of percentages will empower you to make informed decisions and achieve your goals. The simple question "1 is what percent of 30?" serves as a gateway to a deeper understanding of this fundamental mathematical concept and its widespread applications. Remember that consistent practice is key to mastering percentage calculations and becoming proficient in their various applications.
Latest Posts
Latest Posts
-
A Rectangle Has A Height Of And A Width Of
May 11, 2025
-
6 7 Divided By 1 6 As A Fraction
May 11, 2025
-
Greatest Common Factor Of 7 And 28
May 11, 2025
-
How Many Milliliters Are In 15 Ounces
May 11, 2025
-
How Many Days Is 318 Hours
May 11, 2025
Related Post
Thank you for visiting our website which covers about 1 Is What Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.