1 Out Of 12 Is What Percent
Treneri
May 10, 2025 · 5 min read
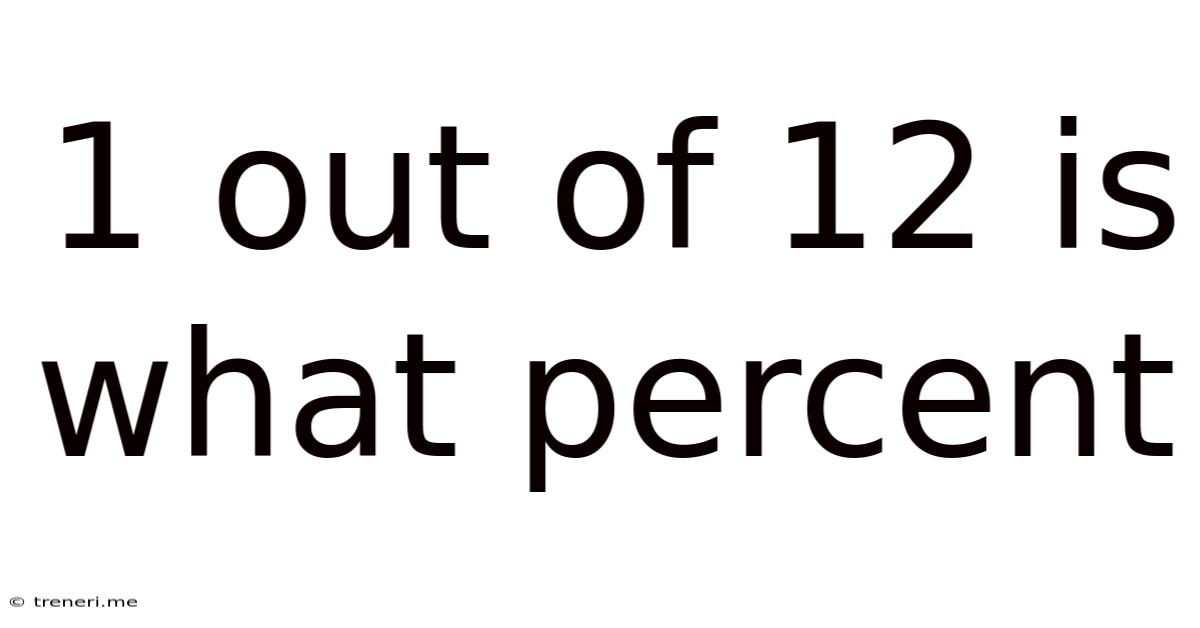
Table of Contents
1 Out of 12 is What Percent? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts and taxes to comprehending statistical data and analyzing financial reports. This comprehensive guide will delve into the intricacies of calculating percentages, focusing specifically on the question: "1 out of 12 is what percent?" We'll explore the calculation process, provide various methods for solving similar problems, and discuss practical applications to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5. This fundamental concept is crucial for solving percentage problems.
Key Terms and Concepts:
- Numerator: The top number in a fraction (in this case, 1).
- Denominator: The bottom number in a fraction (in this case, 12).
- Percentage: The fraction expressed as a value out of 100.
Calculating "1 out of 12" as a Percentage: The Primary Method
The most straightforward approach to calculating "1 out of 12" as a percentage involves two simple steps:
Step 1: Convert the fraction to a decimal:
Divide the numerator (1) by the denominator (12):
1 ÷ 12 = 0.08333... (the 3's repeat infinitely)
Step 2: Convert the decimal to a percentage:
Multiply the decimal by 100:
0.08333... × 100 = 8.333...%
Therefore, 1 out of 12 is approximately 8.33%. The recurring decimal can be rounded to two decimal places for practical purposes.
Alternative Methods for Percentage Calculation
While the primary method is efficient, several alternative approaches can be used to solve percentage problems, particularly those involving fractions. Let's explore a couple of these methods:
Method 2: Using Proportions
This method leverages the concept of ratios and proportions. We set up a proportion where we equate two ratios: the ratio of the part to the whole (1/12) and the ratio of the percentage to 100 (x/100). This can be expressed as:
1/12 = x/100
To solve for 'x' (the percentage), we cross-multiply:
12x = 100
x = 100/12
x ≈ 8.33%
This method provides another pathway to the same solution, reinforcing the underlying mathematical principles.
Method 3: Utilizing a Calculator
Modern calculators are equipped with percentage functions that simplify these calculations considerably. Simply enter the fraction (1/12) and press the percentage button (%) to obtain the result directly. This is the most efficient method for quick calculations.
Practical Applications: Real-World Examples
The ability to calculate percentages extends far beyond simple mathematical exercises. Here are several real-world applications demonstrating the usefulness of this skill:
- Sales and Discounts: If a store offers a discount of 1 out of 12 items purchased, customers can easily determine the percentage discount offered.
- Financial Analysis: Investors use percentage calculations to analyze returns on investment (ROI), track portfolio performance, and assess financial risk.
- Statistical Analysis: Percentages are frequently used in surveys and polls to represent the proportion of respondents who chose a particular option.
- Academic Performance: Grades are often expressed as percentages to indicate the proportion of correct answers achieved in an assessment.
- Data Visualization: Percentages are commonly used in charts and graphs to visually represent data, making trends and patterns easier to understand.
Expanding the Skill Set: Calculating Other Percentages
Once you've mastered the calculation of "1 out of 12," you can easily apply the same principles to other percentage problems. For example:
- 2 out of 12: (2 ÷ 12) × 100 ≈ 16.67%
- 3 out of 12: (3 ÷ 12) × 100 = 25%
- 5 out of 12: (5 ÷ 12) × 100 ≈ 41.67%
The methodology remains consistent: divide the numerator by the denominator and then multiply the result by 100.
Troubleshooting Common Errors and Misconceptions
Several common errors can arise when calculating percentages. Being aware of these pitfalls can help you avoid mistakes:
- Incorrect Order of Operations: Always perform the division before the multiplication. Failing to do so will result in an incorrect answer.
- Rounding Errors: When rounding decimals, consistency is crucial. Rounding prematurely can lead to accumulating errors, affecting the final result.
- Confusing Numerator and Denominator: Make sure you are correctly identifying the numerator (the part) and the denominator (the whole).
Mastering Percentage Calculations: A Continuous Journey
Understanding percentage calculations is not a one-time achievement; it's an ongoing skill-building process. Regular practice and exposure to various applications will reinforce your understanding and improve your proficiency. The more you utilize percentage calculations in different contexts, the more intuitive and effortless the process will become.
Beyond the Basics: Advanced Percentage Applications
The principles discussed above are fundamental. However, understanding percentages extends to more complex scenarios:
- Percentage Increase/Decrease: Calculating the percentage change between two values requires understanding the difference between the two numbers relative to the initial value.
- Compound Interest: This concept involves calculating interest not only on the principal amount but also on accumulated interest from previous periods.
- Percentage Points vs. Percentages: A crucial distinction lies in understanding the difference between a percentage point change and a percentage change.
Conclusion: The Power of Percentage Understanding
The ability to calculate percentages is a critical life skill with far-reaching applications. From managing personal finances to analyzing complex datasets, a strong grasp of percentage calculations empowers you to make informed decisions and effectively communicate quantitative information. By understanding the various methods and practicing regularly, you can master this crucial skill and enhance your ability to navigate the numerical aspects of daily life and professional endeavors. This comprehensive guide serves as a starting point, encouraging you to explore further and expand your knowledge of percentage calculations as you encounter new challenges and applications. Remember, consistent practice is key to mastery.
Latest Posts
Latest Posts
-
How To Convert Joules To Nanometers
May 10, 2025
-
How Many Miles Is 10 Of Gas
May 10, 2025
-
Crown Rump Length Chart In Mm
May 10, 2025
-
What Percentage Of 11 Is 4
May 10, 2025
-
1994 Was How Many Years Ago
May 10, 2025
Related Post
Thank you for visiting our website which covers about 1 Out Of 12 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.