10000 As A Power Of 10
Treneri
May 10, 2025 · 6 min read
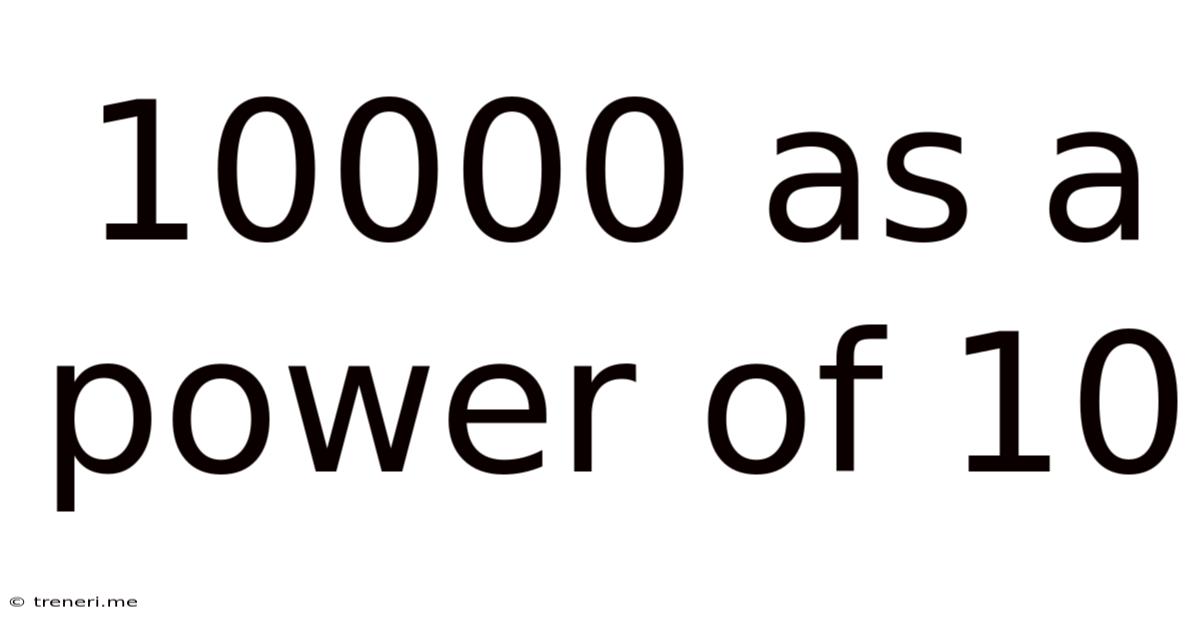
Table of Contents
10,000 as a Power of 10: Exploring Exponential Notation and its Applications
The number 10,000 holds a special place in mathematics, particularly when discussing powers of 10. Understanding this representation is crucial for grasping exponential notation, scientific notation, and its widespread applications across various fields. This article delves deep into the concept of 10,000 as a power of 10, examining its mathematical significance, exploring practical examples, and highlighting its relevance in diverse contexts.
Understanding Exponential Notation
Before we dive into 10,000, let's establish a firm understanding of exponential notation. Exponential notation, also known as scientific notation for very large or very small numbers, is a concise way of representing numbers as a base raised to a power (or exponent). For instance, 10<sup>2</sup> represents 10 multiplied by itself twice (10 x 10 = 100). The base is 10, and the exponent is 2.
The exponent indicates how many times the base is multiplied by itself. A positive exponent signifies repeated multiplication, while a negative exponent implies repeated division. For example:
- 10<sup>3</sup> = 10 x 10 x 10 = 1000
- 10<sup>-2</sup> = 1/10<sup>2</sup> = 1/100 = 0.01
10,000 as a Power of 10: The Core Concept
Now, let's focus on 10,000. To express 10,000 as a power of 10, we need to determine how many times 10 must be multiplied by itself to equal 10,000. This can be easily visualized:
10 x 10 x 10 x 10 = 10,000
Therefore, 10,000 can be represented as 10<sup>4</sup>. The base is 10, and the exponent is 4. This means 10 is multiplied by itself four times.
The Significance of Powers of 10
Powers of 10 are incredibly significant in mathematics and science due to their simplicity and elegance. They provide a convenient way to represent extremely large or small numbers using a compact notation. This is especially useful in fields dealing with vast quantities or microscopic scales:
- Astronomy: Distances between celestial bodies are often expressed in powers of 10, such as light-years (distances of trillions of kilometers).
- Physics: Atomic dimensions and subatomic particle properties are described using negative powers of 10 (e.g., nanometers).
- Computer Science: Data storage capacities (gigabytes, terabytes, petabytes) are usually presented using powers of 10 (or powers of 2, which are closely related).
- Finance: Large sums of money are conveniently expressed using powers of 10 (millions, billions, trillions).
Practical Applications of 10<sup>4</sup>
Understanding 10,000 as 10<sup>4</sup> has numerous practical applications. For instance:
-
Area Calculations: Imagine a square plot of land with sides measuring 100 meters each. The area of this plot is 100 meters x 100 meters = 10,000 square meters, or 10<sup>4</sup> square meters.
-
Volume Calculations: A cubic container with sides of 10 meters each has a volume of 10 meters x 10 meters x 10 meters = 1000 cubic meters, which is 10<sup>3</sup> cubic meters. Ten such containers would have a total volume of 10,000 cubic meters or 10<sup>4</sup> cubic meters.
-
Population Studies: A city with 10,000 inhabitants is conveniently represented as a population of 10<sup>4</sup> individuals.
-
Data Representation: A database holding 10,000 records can be easily described using the exponential notation 10<sup>4</sup>.
Scientific Notation and 10,000
Scientific notation is a specific type of exponential notation used to represent numbers in the form a x 10<sup>b</sup>, where 'a' is a number between 1 and 10 (but not including 10), and 'b' is an integer. While 10,000 is already a relatively small number, it can be expressed in scientific notation as 1.0 x 10<sup>4</sup>. This form is particularly useful when dealing with vastly larger or smaller numbers.
Beyond 10,000: Exploring Higher Powers of 10
Understanding 10,000 as 10<sup>4</sup> provides a stepping stone to understanding higher powers of 10. The pattern continues:
- 10<sup>5</sup> = 100,000 (one hundred thousand)
- 10<sup>6</sup> = 1,000,000 (one million)
- 10<sup>9</sup> = 1,000,000,000 (one billion)
- 10<sup>12</sup> = 1,000,000,000,000 (one trillion)
And so on. Each increase in the exponent adds another zero to the number. This systematic growth makes powers of 10 invaluable for representing and manipulating large numbers efficiently.
Negative Powers of 10 and Their Relevance
Just as we explored positive powers of 10, negative powers are equally important, especially when representing very small numbers. These negative powers represent fractions where the denominator is a power of 10:
- 10<sup>-1</sup> = 0.1 (one-tenth)
- 10<sup>-2</sup> = 0.01 (one-hundredth)
- 10<sup>-3</sup> = 0.001 (one-thousandth)
- 10<sup>-4</sup> = 0.0001 (one ten-thousandth)
These negative powers are frequently used in science and engineering to denote small measurements, such as micrometers or nanometers.
Converting Between Standard and Exponential Notation
Converting numbers between standard notation (the usual way we write numbers) and exponential notation is a fundamental skill. For numbers greater than or equal to 10, count the number of digits to the left of the decimal point, and that number minus one becomes the exponent. For numbers less than 1, the exponent is negative and is found by counting the number of places the decimal point must be moved to the right to obtain a number between 1 and 10.
Examples:
-
5000: Move the decimal point three places to the left to get 5.0. Therefore, 5000 = 5.0 x 10<sup>3</sup>.
-
0.00025: Move the decimal point four places to the right to get 2.5. Therefore, 0.00025 = 2.5 x 10<sup>-4</sup>.
Solving Problems Involving Powers of 10
Many mathematical problems involve manipulating powers of 10. Remember these key rules:
-
Multiplication: When multiplying powers of 10, add the exponents. For example, 10<sup>3</sup> x 10<sup>2</sup> = 10<sup>(3+2)</sup> = 10<sup>5</sup>.
-
Division: When dividing powers of 10, subtract the exponents. For example, 10<sup>5</sup> / 10<sup>2</sup> = 10<sup>(5-2)</sup> = 10<sup>3</sup>.
-
Exponents of Exponents: When raising a power of 10 to another power, multiply the exponents. For example, (10<sup>2</sup>)<sup>3</sup> = 10<sup>(2x3)</sup> = 10<sup>6</sup>.
Mastering these rules is crucial for solving complex calculations involving exponential notation efficiently.
Conclusion: The Ubiquity of 10,000 and its Exponential Representation
Understanding 10,000 as 10<sup>4</sup> is not merely an academic exercise. It is a foundational concept that unlocks a deeper understanding of exponential notation, scientific notation, and their vast applications across numerous fields. From calculating vast distances in astronomy to representing microscopic dimensions in physics, the elegant simplicity of powers of 10 simplifies complex calculations and provides a clear and concise way to represent numbers across an immense range of scales. By grasping the significance of 10<sup>4</sup> and its broader context within exponential notation, you equip yourself with a powerful tool for tackling mathematical and scientific challenges. The ability to seamlessly convert between standard notation and exponential notation is an invaluable skill that will benefit you in various academic and professional pursuits.
Latest Posts
Latest Posts
-
What Size Rock For French Drain
May 10, 2025
-
What Does 1 Part To 3 Parts Mean
May 10, 2025
-
How To Find Perimeter When Given Area
May 10, 2025
-
What Is The Gcf Of 24 And 84
May 10, 2025
-
What Grade Is 12 Out Of 14
May 10, 2025
Related Post
Thank you for visiting our website which covers about 10000 As A Power Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.