15 Is What Percent Of 500
Treneri
Apr 12, 2025 · 4 min read
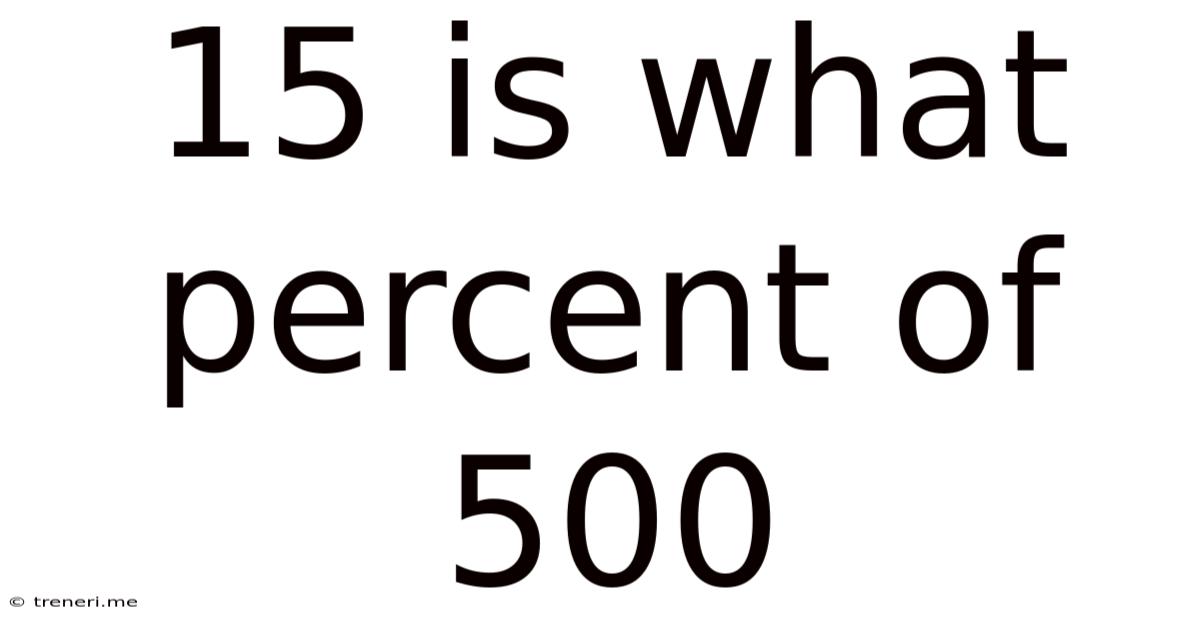
Table of Contents
15 is What Percent of 500? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with applications across various fields, from everyday budgeting to complex financial analysis. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data accurately. This article delves deep into the question, "15 is what percent of 500?", providing a step-by-step explanation, practical examples, and exploring related concepts to solidify your understanding of percentage calculations.
Understanding Percentages
Before we dive into the specific calculation, let's review the basic concept of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 50% means 50 out of 100, which is equivalent to 0.5 or ½.
Percentages are widely used to express proportions, changes, and rates. They provide a standardized way to compare different quantities and easily visualize relative sizes.
Calculating "15 is What Percent of 500?"
Now, let's address the core question: What percentage does 15 represent of 500? We can solve this using a simple formula:
(Part / Whole) * 100 = Percentage
In our case:
- Part: 15
- Whole: 500
Let's plug these values into the formula:
(15 / 500) * 100 = 3%
Therefore, 15 is 3% of 500.
Step-by-Step Calculation with Explanation
To make the process even clearer, let's break down the calculation step-by-step:
-
Divide the part by the whole: 15 / 500 = 0.03
This step determines the decimal equivalent of the fraction representing the proportion of 15 to 500.
-
Multiply the result by 100: 0.03 * 100 = 3
Multiplying by 100 converts the decimal into a percentage. This is because percentages are expressed as parts of 100.
Alternative Methods for Calculating Percentages
While the formula above is the most straightforward, there are other approaches you can use, particularly helpful for mental calculations or when dealing with simpler numbers.
-
Using Proportions: You can set up a proportion to solve for the unknown percentage (x):
15/500 = x/100
Cross-multiply: 15 * 100 = 500 * x
Solve for x: 1500 = 500x => x = 1500/500 = 3
-
Using Decimal Conversion: First, convert the percentage to a decimal by dividing by 100. Then, multiply the decimal by the whole number.
3% = 3/100 = 0.03 0.03 * 500 = 15
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-life scenarios:
- Financial Planning: Calculating interest rates, discounts, taxes, and investment returns all rely on percentages.
- Sales and Marketing: Analyzing sales figures, conversion rates, and market share requires understanding percentages.
- Data Analysis: Percentages are essential for interpreting statistical data and visualizing trends.
- Academic Performance: Calculating grades and overall academic performance often involves percentages.
- Everyday Budgeting: Determining the percentage of income spent on different categories helps manage personal finances effectively.
Advanced Percentage Calculations: Finding the Whole or the Part
The fundamental formula can be rearranged to solve for different unknowns:
-
Finding the Whole (when you know the part and the percentage):
Whole = (Part / Percentage) * 100
For example: If 20% of a number is 10, what is the number?
Whole = (10 / 20) * 100 = 50
-
Finding the Part (when you know the whole and the percentage):
Part = (Percentage/100) * Whole
For example: What is 15% of 200?
Part = (15/100) * 200 = 30
Percentage Increase and Decrease
Another important aspect of percentage calculations involves determining percentage increases and decreases. This is often used to analyze changes over time or compare different values.
-
Percentage Increase: [(New Value - Old Value) / Old Value] * 100
-
Percentage Decrease: [(Old Value - New Value) / Old Value] * 100
For instance, if a price increases from $50 to $60, the percentage increase is:
[(60 - 50) / 50] * 100 = 20%
Troubleshooting Common Mistakes in Percentage Calculations
Many errors occur due to misunderstanding the order of operations or misinterpreting the question. Here are some common pitfalls to avoid:
- Incorrect Order of Operations: Always follow the order of operations (PEMDAS/BODMAS) to ensure accuracy.
- Confusing Part and Whole: Clearly identify which number represents the part and which represents the whole.
- Misunderstanding the Question: Carefully read the problem to determine what information is given and what needs to be calculated.
- Calculation Errors: Double-check your calculations to avoid simple arithmetic mistakes.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is an invaluable skill that enhances your ability to analyze data, make informed decisions, and understand the world around you more effectively. This article has provided a comprehensive guide, covering the fundamentals, various calculation methods, real-world applications, and common pitfalls to avoid. By understanding these concepts and practicing regularly, you'll confidently tackle any percentage-related problem that comes your way. Remember, the key is to grasp the underlying principles and apply the appropriate formulas correctly. With consistent practice and a clear understanding of the concepts, percentage calculations will become second nature.
Latest Posts
Latest Posts
-
21 8 As A Mixed Number
May 09, 2025
-
16 Ft By 42 Inch Pool Gallons
May 09, 2025
-
What Is The Gcf Of 36 And 16
May 09, 2025
-
What Grade Is A 27 Out Of 35
May 09, 2025
-
What Is The Greatest Common Factor Of 36 And 84
May 09, 2025
Related Post
Thank you for visiting our website which covers about 15 Is What Percent Of 500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.