21 8 As A Mixed Number
Treneri
May 09, 2025 · 4 min read
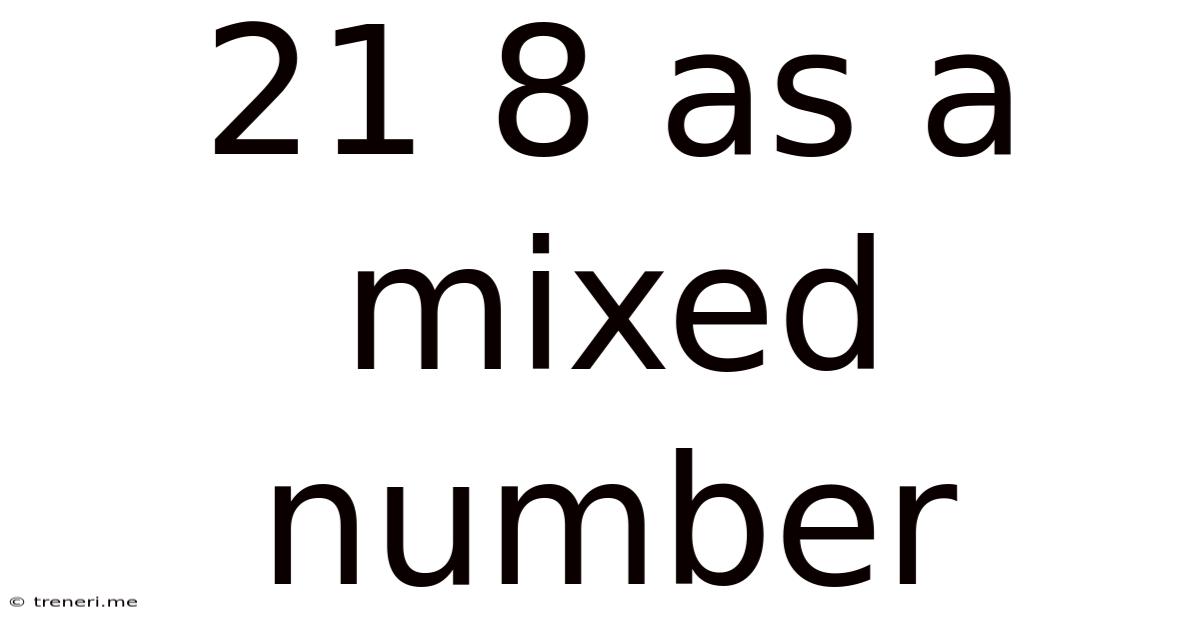
Table of Contents
21/8 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve deep into converting the improper fraction 21/8 into a mixed number, explaining the process step-by-step and providing additional examples to solidify your understanding. We'll also explore the practical applications of this conversion and offer tips for tackling similar problems.
What is a Mixed Number?
Before we dive into converting 21/8, let's define what a mixed number is. A mixed number is a combination of a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number; 2 is the whole number, and ¾ is the proper fraction. An improper fraction, on the other hand, has a numerator that is greater than or equal to the denominator. Our focus, 21/8, is an example of an improper fraction.
Converting 21/8 to a Mixed Number: The Step-by-Step Process
Converting an improper fraction to a mixed number involves dividing the numerator by the denominator. Here's how we do it for 21/8:
-
Divide the numerator by the denominator: We divide 21 (the numerator) by 8 (the denominator).
21 ÷ 8 = 2 with a remainder of 5
-
The quotient becomes the whole number: The result of the division (the quotient) is 2. This becomes the whole number part of our mixed number.
-
The remainder becomes the numerator of the proper fraction: The remainder of the division is 5. This becomes the numerator of the proper fraction in our mixed number.
-
The denominator remains the same: The denominator of the improper fraction (8) remains the same in the proper fraction of the mixed number.
-
Combine the whole number and the proper fraction: Putting it all together, we get the mixed number: 2 ⅝
Therefore, 21/8 as a mixed number is 2 ⅝.
Visual Representation: Understanding the Conversion
Imagine you have 21 slices of pizza, and each pizza has 8 slices. You can make 2 full pizzas (2 x 8 = 16 slices) and have 5 slices left over. This leftover 5 slices represent the 5/8 of a pizza. This visual representation helps solidify the concept of 21/8 being equivalent to 2 ⅝.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in everyday life and various fields:
-
Cooking and Baking: Recipes often call for amounts expressed as mixed numbers (e.g., 2 ½ cups of flour).
-
Measurement: Measuring length, weight, or volume often involves mixed numbers (e.g., 3 ¼ inches).
-
Construction and Engineering: Precise measurements in construction and engineering projects require the use of mixed numbers for accurate calculations.
-
Data Analysis: Representing data and fractions in a more easily understood format often uses mixed numbers.
More Examples of Converting Improper Fractions to Mixed Numbers
Let's practice converting a few more improper fractions to mixed numbers to reinforce the process:
-
17/5: 17 ÷ 5 = 3 with a remainder of 2. Therefore, 17/5 = 3 ⅖
-
26/3: 26 ÷ 3 = 8 with a remainder of 2. Therefore, 26/3 = 8 ⅔
-
35/6: 35 ÷ 6 = 5 with a remainder of 5. Therefore, 35/6 = 5 ⅚
-
41/9: 41 ÷ 9 = 4 with a remainder of 5. Therefore, 41/9 = 4 ⅝
Converting Mixed Numbers Back to Improper Fractions
It's also important to understand the reverse process: converting a mixed number back to an improper fraction. This involves:
-
Multiply the whole number by the denominator: For example, with 2 ⅝, we multiply 2 (whole number) by 8 (denominator) = 16.
-
Add the numerator: Add the result from step 1 to the numerator (5): 16 + 5 = 21.
-
Keep the denominator the same: The denominator remains 8.
Therefore, 2 ⅝ becomes 21/8.
Troubleshooting Common Mistakes
When converting improper fractions to mixed numbers, common mistakes include:
-
Incorrect division: Double-check your division to ensure accuracy.
-
Misplacing the remainder: The remainder is crucial; ensure it's correctly used as the numerator of the proper fraction.
-
Forgetting the denominator: The denominator of the original improper fraction stays the same in the mixed number's fraction.
Tips for Success
-
Practice regularly: Consistent practice is key to mastering fraction conversion.
-
Use visual aids: Diagrams and real-world examples can help conceptualize the process.
-
Check your work: Always verify your answer to ensure accuracy.
-
Utilize online resources: There are many online tools and calculators available for extra help and practice.
Conclusion
Converting improper fractions to mixed numbers is a vital skill with numerous applications. By understanding the step-by-step process, practicing regularly, and utilizing the tips provided, you can confidently convert fractions and enhance your mathematical abilities. Remember, the key is to master the division process and correctly interpret the quotient and remainder to create the equivalent mixed number. Through practice and understanding, you'll become proficient in handling fractions and mixed numbers in any context. Now, go forth and conquer those fractions!
Latest Posts
Latest Posts
-
Formula For Finding The Base Of A Triangle
May 10, 2025
-
Born In 1996 How Old In 2023
May 10, 2025
-
What Percent Of 7 Is 4
May 10, 2025
-
How Many Minutes Are In 6 Years
May 10, 2025
-
62 20 Rounded To The Nearest Tenth
May 10, 2025
Related Post
Thank you for visiting our website which covers about 21 8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.