15 Is What Percent Of 90
Treneri
May 10, 2025 · 4 min read
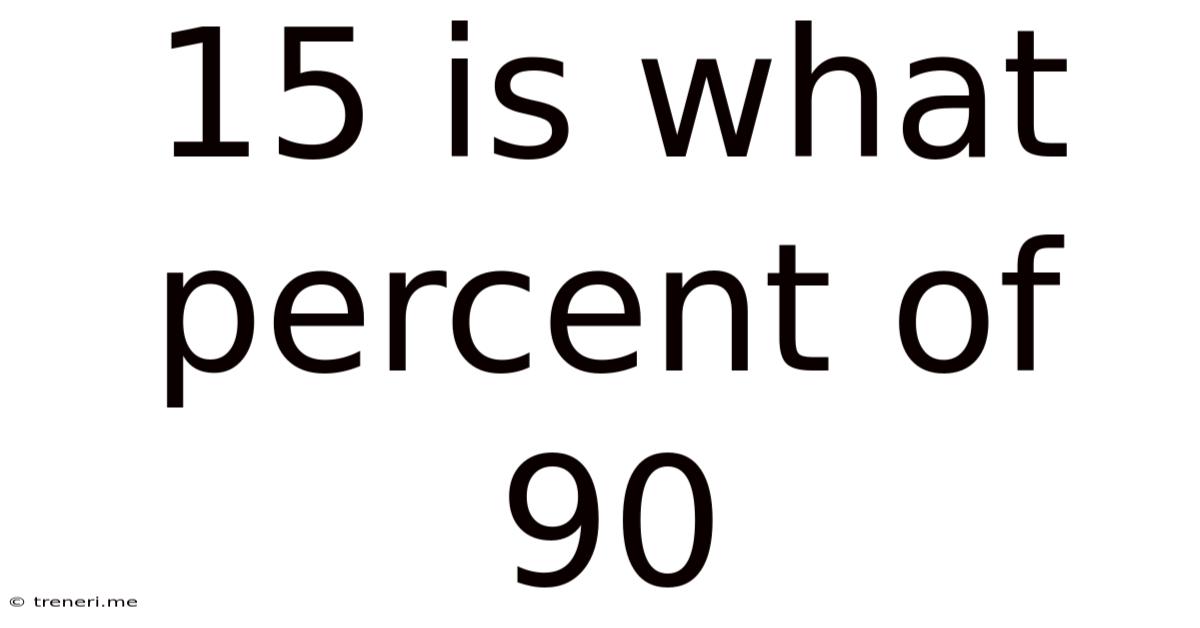
Table of Contents
15 is What Percent of 90: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and taxes to understanding statistics and financial data. This article delves deep into the question, "15 is what percent of 90?", providing not only the answer but a comprehensive explanation of the underlying concepts and various methods for solving percentage problems. We'll also explore real-world applications and delve into advanced percentage calculations.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." For instance, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25. Understanding this fundamental relationship is crucial to solving any percentage problem.
Key Terms and Concepts:
- Percentage: The number expressed as a fraction of 100 (e.g., 15%).
- Part: The number that represents a portion of the whole (e.g., 15).
- Whole: The total number or the base amount (e.g., 90).
Method 1: Using the Percentage Formula
The most common method for calculating percentages involves using a straightforward formula:
(Part / Whole) * 100 = Percentage
In our specific problem, "15 is what percent of 90?", we can identify the parts as follows:
- Part: 15
- Whole: 90
Substituting these values into the formula:
(15 / 90) * 100 = Percentage
Calculating this:
(0.1667) * 100 = 16.67%
Therefore, 15 is 16.67% of 90.
Method 2: Using Proportions
Another effective approach involves setting up a proportion:
Part / Whole = Percentage / 100
Again, using our values:
15 / 90 = x / 100
To solve for 'x' (the percentage), we cross-multiply:
15 * 100 = 90 * x
1500 = 90x
x = 1500 / 90
x = 16.67%
This method confirms that 15 is 16.67% of 90.
Method 3: Using Decimal Conversion
This method involves converting the percentage to a decimal and then multiplying it by the whole number. While not directly answering "15 is what percent of 90?", it helps demonstrate the relationship between percentages and decimals and can be used to solve similar problems. To find what percentage 15 represents of 90, we would perform the following calculation:
- Divide the part by the whole: 15 / 90 = 0.1667
- Multiply the result by 100 to convert it back to a percentage: 0.1667 * 100 = 16.67%
This reinforces the result that 15 is 16.67% of 90.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is vital in numerous real-world scenarios:
1. Finance and Budgeting:
- Calculating interest rates: Understanding how interest is calculated on loans, savings accounts, and investments is crucial for making informed financial decisions.
- Analyzing financial statements: Financial reports often use percentages to express key metrics like profit margins, revenue growth, and debt ratios.
- Determining discounts and sales tax: Calculating discounts during sales and determining the total cost of purchases including sales tax both involve percentage calculations.
2. Statistics and Data Analysis:
- Interpreting statistical data: Percentages are widely used in presenting statistical data, such as population demographics, survey results, and research findings.
- Calculating probabilities: Probability, a crucial concept in statistics, often involves expressing probabilities as percentages.
- Understanding data visualization: Charts and graphs frequently use percentages to represent proportions and trends in data.
3. Everyday Life:
- Calculating tips and gratuities: Calculating the appropriate tip at a restaurant or for a service provider involves using percentages.
- Understanding nutritional information: Food labels often use percentages to indicate the percentage of daily recommended values for different nutrients.
- Evaluating sales and discounts: Making informed purchase decisions during sales requires understanding and calculating percentage discounts.
Advanced Percentage Calculations: Beyond the Basics
While the basic percentage formula is sufficient for many situations, understanding more complex percentage calculations can be valuable. This section explores some advanced concepts.
1. Calculating Percentage Increase or Decrease:
Determining the percentage change between two numbers requires a slightly modified formula:
[(New Value - Old Value) / Old Value] * 100 = Percentage Change
A positive result indicates a percentage increase, while a negative result indicates a percentage decrease.
2. Calculating Percentage Points:
Percentage points represent the difference between two percentages. It's crucial not to confuse this with a percentage change. For instance, if the interest rate rises from 5% to 8%, the increase is 3 percentage points, not a 60% increase.
3. Working with Compound Percentages:
Compound percentages involve calculating percentages on percentages, often encountered in interest calculations where interest is earned on both the principal and accumulated interest. These calculations require iterative computations or the use of compound interest formulas.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is essential for navigating various aspects of life, from personal finance to professional endeavors. By understanding the fundamental concepts and applying different calculation methods, you can confidently tackle a wide range of percentage problems. This article provides a solid foundation for understanding percentages, equipping you with the skills to handle both simple and more complex percentage calculations with accuracy and efficiency. Remember to practice regularly to further enhance your understanding and proficiency.
Latest Posts
Latest Posts
-
Do You Lose Calories In The Sauna
May 11, 2025
-
Highest Common Factor Of 14 And 49
May 11, 2025
-
Can You Tan In A Uv Of 6
May 11, 2025
-
A Rectangle Has A Height Of And A Width Of
May 11, 2025
-
6 7 Divided By 1 6 As A Fraction
May 11, 2025
Related Post
Thank you for visiting our website which covers about 15 Is What Percent Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.