16/5 Divided By 4/25 In Simplest Form
Treneri
May 10, 2025 · 4 min read
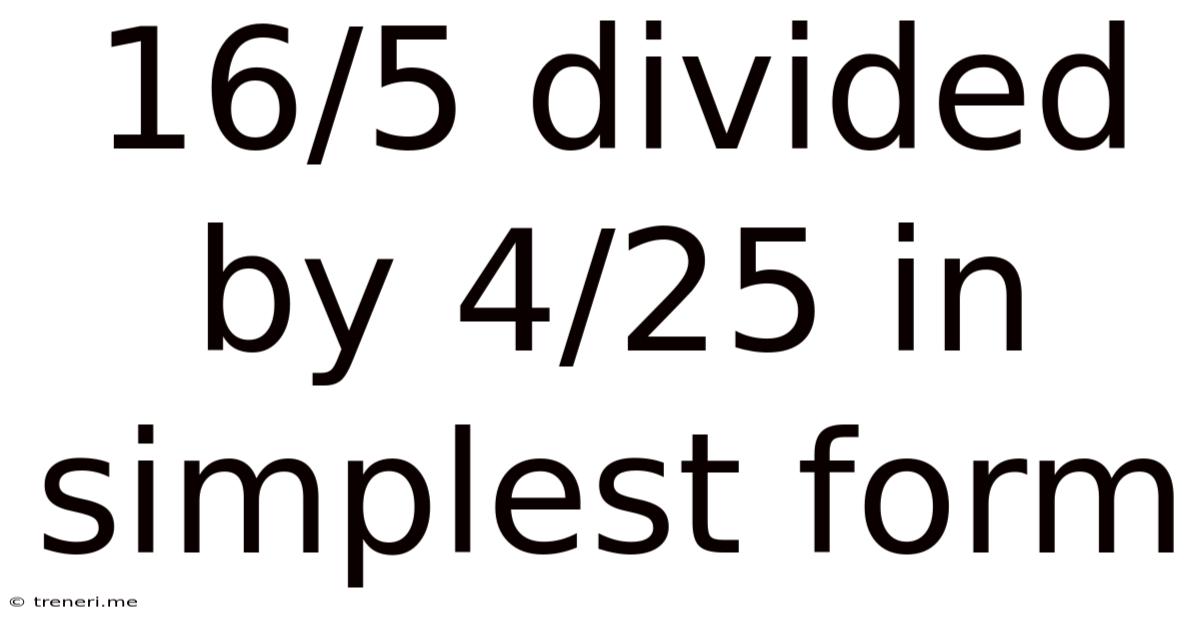
Table of Contents
16/5 Divided by 4/25 in Simplest Form: A Comprehensive Guide
This article will delve into the process of dividing fractions, specifically tackling the problem of 16/5 divided by 4/25. We'll break down the steps, explain the underlying concepts, and explore various methods to arrive at the simplest form of the answer. Understanding fraction division is crucial in various fields, from basic arithmetic to advanced mathematics and even everyday life applications. This guide is designed to be comprehensive, ensuring a thorough understanding of the process, regardless of your prior mathematical background.
Understanding Fraction Division
Before jumping into the specific problem, let's review the fundamental concept of dividing fractions. Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 4/25 is 25/4.
This rule simplifies the division process significantly. Instead of directly dividing fractions, we transform the division problem into a multiplication problem, making the calculation much easier to manage.
Step-by-Step Solution: 16/5 ÷ 4/25
Let's apply this knowledge to solve 16/5 divided by 4/25:
-
Find the reciprocal of the second fraction: The reciprocal of 4/25 is 25/4.
-
Change the division to multiplication: Our problem now becomes 16/5 * 25/4.
-
Multiply the numerators: Multiply the top numbers (numerators) together: 16 * 25 = 400.
-
Multiply the denominators: Multiply the bottom numbers (denominators) together: 5 * 4 = 20.
-
Form the new fraction: This gives us a new fraction: 400/20.
-
Simplify the fraction: To express the answer in its simplest form, we need to find the greatest common divisor (GCD) of the numerator (400) and the denominator (20). The GCD of 400 and 20 is 20. We divide both the numerator and the denominator by the GCD:
400 ÷ 20 = 20 20 ÷ 20 = 1
-
Final Answer: The simplest form of 16/5 divided by 4/25 is 20.
Alternative Methods for Solving Fraction Division
While the above method is the most straightforward, let's explore some alternative approaches that can be beneficial depending on the complexity of the fractions involved.
Method 1: Cancellation Before Multiplication
This method involves simplifying the fractions before performing the multiplication. It can significantly reduce the size of the numbers you're working with and make the calculation simpler.
Let's revisit the problem: 16/5 ÷ 4/25 = 16/5 * 25/4
Notice that 16 and 4 share a common factor of 4, and 25 and 5 share a common factor of 5. We can cancel these common factors:
(16/4) * (25/5) = 4 * 5 = 20
This method leads to the same answer (20) but involves smaller numbers, making it less prone to errors.
Method 2: Converting to Decimal (Less Precise)
While generally less preferred for maintaining accuracy, especially with more complex fractions, it's possible to convert the fractions to decimals before dividing.
16/5 = 3.2 4/25 = 0.16
3.2 ÷ 0.16 = 20
This method provides the correct answer but introduces the potential for rounding errors if dealing with fractions that don't have exact decimal equivalents.
Real-World Applications of Fraction Division
Understanding fraction division isn't just a theoretical exercise; it has numerous practical applications in everyday life:
-
Cooking and Baking: Scaling recipes up or down often requires dividing or multiplying fractions. For example, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you'll need to divide 1/2 by 2.
-
Construction and Measurement: Precise measurements are crucial in construction, and many measurements involve fractions of inches or feet. Dividing fractions is essential for accurate calculations.
-
Sewing and Fabric: Cutting and sewing fabric often involves working with fractional measurements. Dividing fractions helps ensure accurate cuts and proper garment construction.
-
Finance and Budgeting: Dividing fractions can be useful in calculating portions of budgets or splitting costs among multiple people.
-
Data Analysis: In many data analysis tasks, you might need to work with fractional representations of data. Understanding fraction division allows for more accurate and efficient analysis.
Expanding on Fraction Operations: Beyond Division
While this article focuses on division, mastering fractions requires a solid understanding of all four basic operations: addition, subtraction, multiplication, and division. Each operation has its own set of rules and techniques, and proficiency in all four is vital for various mathematical contexts.
Addition and Subtraction: To add or subtract fractions, you must find a common denominator. Once you have a common denominator, you simply add or subtract the numerators.
Multiplication: Multiplying fractions involves multiplying the numerators together and the denominators together. This is often simpler than addition and subtraction.
Conclusion
Dividing fractions, as illustrated with the example 16/5 ÷ 4/25, is a fundamental mathematical skill. By understanding the concept of reciprocals and applying the appropriate methods, you can confidently solve such problems and apply this knowledge to a wide range of real-world scenarios. Mastering fraction division builds a strong foundation for more advanced mathematical concepts and problem-solving. Remember to always simplify your answer to its lowest terms for the most accurate and efficient representation. Practice consistently, and you'll quickly become proficient in handling fractions with ease.
Latest Posts
Latest Posts
-
10000 As A Power Of 10
May 10, 2025
-
Como Saber Si Un Chihuahua Va A Ser Pequeno
May 10, 2025
-
Calculating Enthalpy Of Vaporization From Vapor Pressure
May 10, 2025
-
How Many Days Since May 21 2023
May 10, 2025
-
Cuantos Dias Faltan Para 6 De Agosto
May 10, 2025
Related Post
Thank you for visiting our website which covers about 16/5 Divided By 4/25 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.