2/3 Divided By 1/2 As A Fraction
Treneri
May 09, 2025 · 5 min read
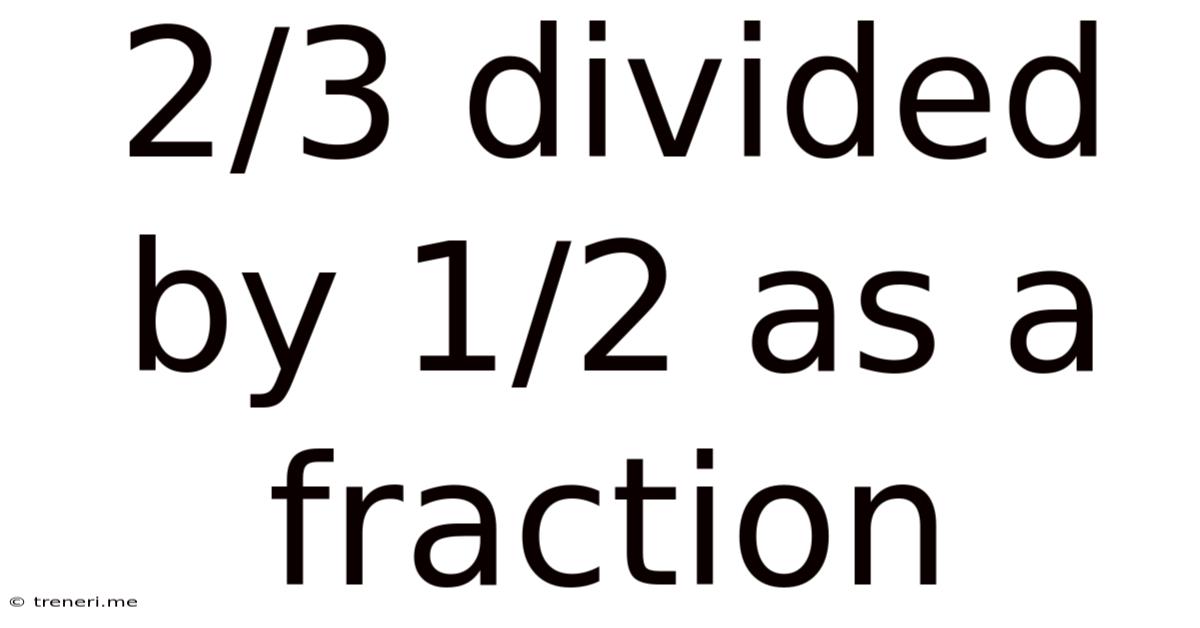
Table of Contents
2/3 Divided by 1/2 as a Fraction: A Comprehensive Guide
Understanding fraction division can be tricky, but mastering it unlocks a powerful tool for solving a wide range of mathematical problems. This comprehensive guide will walk you through the process of dividing 2/3 by 1/2, explaining the underlying concepts and providing various methods to reach the solution. We'll explore the "keep, change, flip" method, the reciprocal method, and visually represent the division using diagrams. By the end, you'll not only know the answer but also understand why it's the answer, solidifying your understanding of fraction division.
Understanding Fraction Division
Before diving into the specific problem of 2/3 divided by 1/2, let's establish a strong foundation in fraction division. When we divide fractions, we're essentially asking, "How many times does one fraction fit into another?" This differs from fraction multiplication, where we're finding a portion of a portion.
Think of it this way: if you have 2 pizzas, and each pizza is cut into thirds (2/3), and you want to know how many halves (1/2) you can get from those two-thirds, you're performing a division.
Method 1: The "Keep, Change, Flip" Method (or Keep, Switch, Flip)
This is arguably the most popular and easiest method for dividing fractions. It involves three simple steps:
- Keep: Keep the first fraction exactly as it is (the dividend).
- Change: Change the division sign to a multiplication sign.
- Flip: Flip (or invert) the second fraction (the divisor), finding its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down (numerator becomes denominator and vice versa).
Let's apply this to our problem: 2/3 ÷ 1/2
- Keep: 2/3
- Change: ÷ becomes ×
- Flip: 1/2 becomes 2/1 (or simply 2)
Now, we have: 2/3 × 2/1
Multiplying fractions is straightforward: multiply the numerators together and the denominators together:
(2 × 2) / (3 × 1) = 4/3
Therefore, 2/3 ÷ 1/2 = 4/3 This can also be expressed as a mixed number: 1 1/3.
Method 2: The Reciprocal Method
This method is essentially the same as the "keep, change, flip" method, but it emphasizes the concept of reciprocals. We understand that dividing by a fraction is the same as multiplying by its reciprocal.
The reciprocal of 1/2 is 2/1 (or 2). So, the problem becomes:
2/3 × 2/1 = 4/3 = 1 1/3
This method highlights the mathematical principle at play, reinforcing the understanding of reciprocals.
Visual Representation: Understanding Division with Diagrams
While the above methods provide an efficient way to solve the problem, visualizing the division can enhance understanding. Imagine a rectangle representing one whole.
Representing 2/3: Divide the rectangle into three equal parts and shade two of them. This represents 2/3.
Dividing by 1/2: Now, we want to see how many halves fit into those two-thirds. Divide the rectangle in half horizontally. You'll notice that a half fits completely within the shaded area, and a significant portion of another half is also within the shaded area.
This visual representation clearly shows that more than one half fits into two-thirds, confirming our answer of 4/3 (or 1 1/3). While not a precise calculation method, it provides an intuitive understanding of the division.
Working with More Complex Fraction Divisions
The methods discussed above are applicable to all fraction divisions. Let's consider a more complex example: 5/8 ÷ 3/4
Using the "keep, change, flip" method:
- Keep: 5/8
- Change: ÷ becomes ×
- Flip: 3/4 becomes 4/3
Now we have: 5/8 × 4/3
Multiplying: (5 × 4) / (8 × 3) = 20/24
We can simplify this fraction by dividing both numerator and denominator by their greatest common divisor, which is 4:
20/24 = 5/6
Therefore, 5/8 ÷ 3/4 = 5/6
Real-World Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it has practical applications in numerous real-world scenarios:
-
Cooking and Baking: Scaling recipes up or down requires fraction division. If a recipe calls for 1/2 cup of flour, and you want to make three times the recipe, you'd need to calculate 3 ÷ 1/2 = 6 cups of flour.
-
Construction and Engineering: Precise measurements and calculations in construction often involve fractions, and dividing fractions is essential for determining the correct quantities of materials.
-
Sewing and Crafting: Cutting fabric or other materials into specific portions requires dividing fractions to ensure accurate measurements.
-
Data Analysis: In data analysis and statistics, dealing with fractions and their divisions is common when working with proportions and ratios.
Common Mistakes to Avoid
When dividing fractions, several common errors can lead to incorrect answers:
-
Forgetting to flip the second fraction: This is the most frequent mistake. Remember the "keep, change, flip" rule.
-
Incorrectly multiplying or simplifying fractions: Ensure that you multiply numerators and denominators correctly and simplify the resulting fraction to its lowest terms.
-
Confusing division with multiplication: Keep the operations distinct; division involves flipping the second fraction before multiplication.
Conclusion
Dividing fractions, while initially appearing daunting, is a manageable process once the underlying principles are understood. The "keep, change, flip" and reciprocal methods provide efficient pathways to solving these problems. Visualizing the division through diagrams can further solidify comprehension. By practicing these methods and understanding the real-world applications, you’ll build confidence and proficiency in handling fraction divisions with ease. Remember to practice regularly to enhance your skills and avoid common errors. With consistent practice, you'll master this essential mathematical skill, equipping you to tackle more complex mathematical challenges.
Latest Posts
Latest Posts
-
11 Pound Ham Feeds How Many
May 09, 2025
-
Tabla De Calorias Completa Y Peso Ideal
May 09, 2025
-
How To Find The Center Of A Sphere
May 09, 2025
-
4 Is 20 Percent Of What Number
May 09, 2025
-
Cuanto Falta Para El 23 De Agosto
May 09, 2025
Related Post
Thank you for visiting our website which covers about 2/3 Divided By 1/2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.