2 3 Times What Equals 1
Treneri
May 13, 2025 · 5 min read
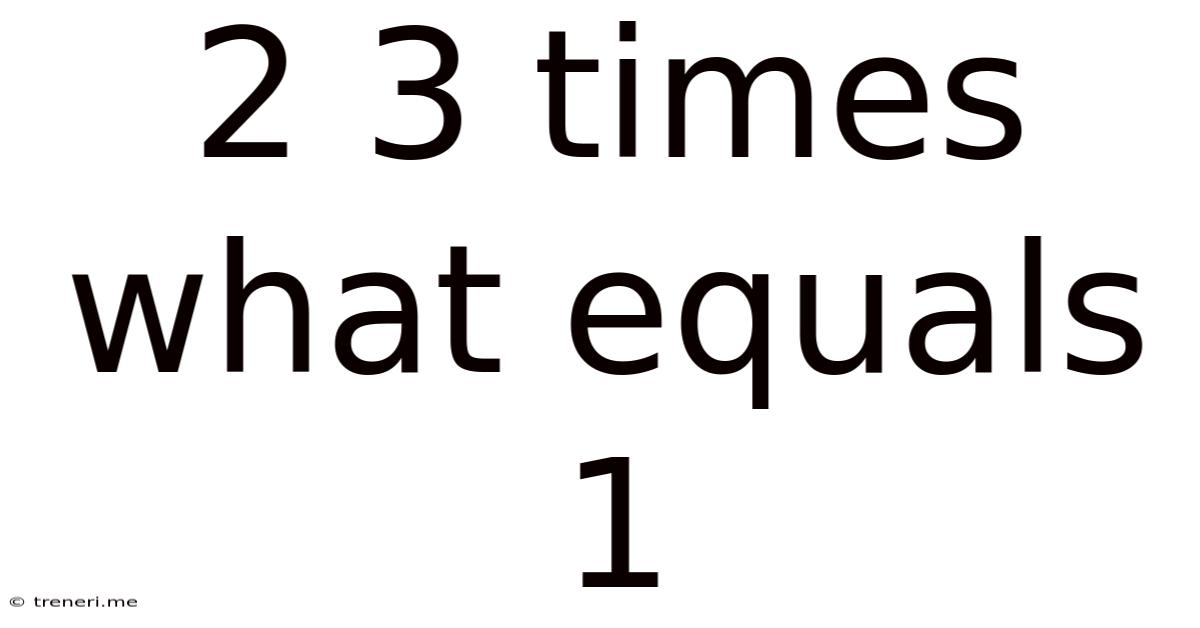
Table of Contents
2, 3 Times What Equals 1? Unlocking the Power of Reciprocals and Inverse Operations
The seemingly simple question, "2, 3 times what equals 1?" actually unlocks a fundamental concept in mathematics: reciprocals and their role in solving equations. This seemingly basic equation holds the key to understanding more complex algebraic manipulations and problem-solving strategies. Let's delve into the solution, explore the underlying mathematical principles, and examine its practical applications.
Understanding the Problem: 2/3 x ? = 1
The question "2/3 times what equals 1" can be mathematically represented as:
(2/3) * x = 1
Where 'x' represents the unknown value we are trying to find. This is a simple algebraic equation, and solving for 'x' requires understanding the concept of inverse operations.
Solving the Equation: The Power of Inverse Operations
To isolate 'x' and find its value, we need to perform the inverse operation of multiplication—division. Since the equation involves multiplying x by 2/3, we need to divide both sides of the equation by 2/3:
x = 1 ÷ (2/3)
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. The reciprocal of 2/3 is 3/2. Therefore:
x = 1 * (3/2)
x = 3/2
or
x = 1.5
Therefore, 2/3 times 1.5 equals 1.
The Concept of Reciprocals: Flipping Fractions for Solutions
The solution hinges on the critical concept of reciprocals. A reciprocal, also known as a multiplicative inverse, is a number that, when multiplied by the original number, results in 1. For any non-zero number 'a', its reciprocal is 1/a.
- Example: The reciprocal of 5 is 1/5 (because 5 * (1/5) = 1).
- Example: The reciprocal of 2/3 is 3/2 (because (2/3) * (3/2) = 1).
- Example: The reciprocal of -4 is -1/4 (because -4 * (-1/4) = 1).
Understanding reciprocals is essential for solving various mathematical problems, including those involving fractions, equations, and even more advanced concepts in algebra and calculus.
Expanding the Concept: Applications in Real-World Scenarios
The seemingly simple equation (2/3) * x = 1 has far-reaching implications in various real-world applications. Let's explore a few examples:
1. Scaling and Proportions:
Imagine you're scaling a recipe. A recipe calls for 2/3 cups of flour, and you want to make a full batch (representing 1 unit). To figure out how much of the recipe to use, you can set up the equation:
(2/3) * x = 1
Solving for x gives you 1.5, meaning you need to use 1.5 times the amount of each ingredient to make a complete batch.
2. Unit Conversions:
In unit conversions, reciprocals play a crucial role. For instance, if you know that 2/3 of a yard is equal to a certain length, and you want to find the total length of one yard, you use the same principle.
3. Percentage Calculations:
Percentages are inherently related to fractions. If 2/3 of a quantity represents 66.67%, then finding the whole quantity (100%) involves using the reciprocal.
4. Financial Calculations:
Reciprocals are used extensively in finance. For instance, calculating the payback period of an investment or determining the return on investment (ROI) often uses similar mathematical principles.
Beyond the Basics: Extending the Concept to More Complex Equations
The principles demonstrated in solving (2/3) * x = 1 extend to more complex equations. The same logic of using inverse operations and reciprocals applies:
- Equations with multiple terms: For instance, solving for 'x' in the equation 2x + 5 = 15 involves using inverse operations to isolate 'x'.
- Equations with variables on both sides: Equations like 3x + 7 = 5x - 3 require rearranging terms before applying inverse operations.
- Equations with fractions: Equations involving multiple fractions require finding a common denominator before solving.
Mastering the fundamental concept of reciprocals and inverse operations provides a solid foundation for tackling these more advanced algebraic equations.
Practical Tips and Tricks for Solving Equations
Here are some practical tips to aid in your equation-solving journey:
- Simplify first: Before performing any operations, simplify the equation as much as possible by combining like terms.
- Isolate the variable: The goal is always to isolate the variable (the unknown, usually represented by 'x', 'y', or other letters) on one side of the equation.
- Perform the same operation on both sides: Remember, whatever operation you perform on one side of the equation must also be performed on the other side to maintain balance.
- Check your answer: Always substitute your calculated value back into the original equation to verify its accuracy. This helps identify any mistakes in the calculation process.
- Practice Regularly: The best way to master solving equations is through regular practice. Start with simple equations and gradually increase the complexity.
Conclusion: Unlocking Mathematical Power
The simple question "2/3 times what equals 1?" serves as a gateway to a deeper understanding of fundamental mathematical concepts—reciprocals and inverse operations. These concepts are not just confined to basic algebra; they form the bedrock for more advanced mathematical studies and are extensively applied in numerous real-world scenarios. By understanding and mastering these principles, you'll significantly enhance your problem-solving abilities and gain a firmer grasp of the mathematical world around you. So, the next time you encounter a seemingly simple equation, remember the power of reciprocals and the elegance of inverse operations. They hold the key to unlocking mathematical solutions.
Latest Posts
Latest Posts
-
How Many Packages Of Shingles In A Square
May 13, 2025
-
800 000 Rounded To The Nearest Hundred Thousand
May 13, 2025
-
How Much Salt For Salt Water Pool
May 13, 2025
-
12 Trillion Divided By 300 Million
May 13, 2025
-
Fractions That Are Equivalent To 8 12
May 13, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Times What Equals 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.