25 Is 60 Percent Of What Number
Treneri
May 14, 2025 · 4 min read
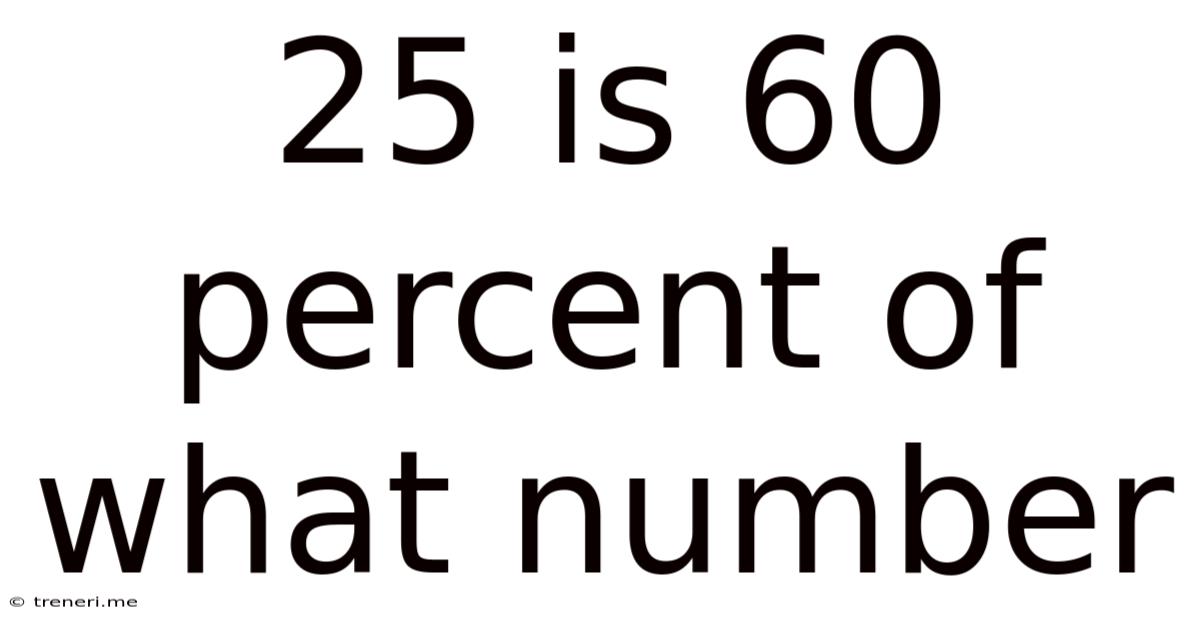
Table of Contents
25 is 60 Percent of What Number? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill in various aspects of life, from calculating discounts and taxes to analyzing data and making financial decisions. This comprehensive guide will walk you through solving the problem "25 is 60 percent of what number?" and explore the broader concept of percentage calculations, equipping you with the knowledge and tools to tackle similar problems with confidence.
Understanding Percentages
A percentage is a fraction or ratio expressed as a portion of 100. It represents a part of a whole. The symbol "%" is used to denote percentages. For example, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
Solving "25 is 60 Percent of What Number?"
This problem can be solved using several methods. We'll explore the most common and straightforward approaches:
Method 1: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
In this case, we know the "Part" (25) and the "Percentage" (60%). We need to find the "Whole". Let's represent the unknown "Whole" with the variable 'x'. We can rewrite the formula as:
25 / x * 100 = 60
To solve for 'x', we can follow these steps:
- Divide both sides by 100: 25 / x = 0.6
- Multiply both sides by x: 25 = 0.6x
- Divide both sides by 0.6: x = 25 / 0.6
- Calculate the result: x ≈ 41.67
Therefore, 25 is 60 percent of approximately 41.67.
Method 2: Using Proportions
Another effective method involves setting up a proportion:
25/x = 60/100
This proportion states that the ratio of 25 to the unknown number (x) is equal to the ratio of 60 to 100. To solve this proportion, we can cross-multiply:
25 * 100 = 60 * x
2500 = 60x
x = 2500 / 60
x ≈ 41.67
This method confirms our previous result.
Expanding on Percentage Calculations: Different Scenarios and Applications
The ability to calculate percentages is crucial in many real-world applications. Let's explore some common scenarios and how to tackle them:
1. Calculating Percentage Increase or Decrease
Percentage change is used to quantify the relative difference between two values. The formula is:
((New Value - Old Value) / Old Value) * 100 = Percentage Change
For example, if the price of an item increased from $50 to $60, the percentage increase is:
((60 - 50) / 50) * 100 = 20%
2. Finding a Percentage of a Number
This involves calculating a specific portion of a given number. For instance, finding 20% of 150:
0.20 * 150 = 30
3. Determining the Original Value After a Percentage Change
This requires working backward from the result of a percentage change. For example, if an item is discounted by 15% and costs $85 after the discount, what was the original price?
Let 'x' be the original price. The equation would be:
x - 0.15x = 85
0.85x = 85
x = 85 / 0.85
x = 100
The original price was $100.
4. Applications in Finance and Business
Percentages are fundamental in financial calculations:
- Interest rates: Calculating simple and compound interest.
- Profit margins: Determining the profitability of a business.
- Investment returns: Measuring the performance of investments.
- Taxes: Computing sales tax, income tax, etc.
- Discounts and markups: Calculating prices after discounts or markups.
5. Applications in Data Analysis and Statistics
Percentages play a critical role in data analysis and interpretation:
- Frequency distributions: Representing data in terms of percentages.
- Statistical measures: Calculating percentages for various statistics (e.g., percentiles).
- Data visualization: Using charts and graphs to represent data as percentages.
Practical Tips and Tricks for Percentage Calculations
- Convert percentages to decimals: It simplifies calculations (e.g., 60% = 0.60).
- Use a calculator: For complex calculations, a calculator is highly recommended.
- Check your work: Verify your results using different methods to ensure accuracy.
- Practice regularly: Consistent practice builds proficiency and confidence.
- Understand the context: Pay attention to the specific details of the problem to choose the appropriate method.
Advanced Percentage Problems and Solutions
Let's delve into a few more complex percentage problems:
Problem 1: After a 10% increase, a quantity becomes 121. What was the original quantity?
Let 'x' be the original quantity. The equation is:
x + 0.10x = 121
1.10x = 121
x = 121 / 1.10
x = 110
The original quantity was 110.
Problem 2: A mixture contains 40% water and 60% alcohol. If the mixture weighs 50 grams, what is the weight of the alcohol?
Weight of alcohol = 0.60 * 50 grams = 30 grams
Conclusion: Mastering Percentages for Real-World Success
Mastering percentage calculations is a valuable skill that enhances your ability to solve problems in various fields. This guide has provided a comprehensive overview of the topic, from basic concepts to advanced applications. By understanding the underlying principles and practicing regularly, you can confidently handle percentage-related tasks and make informed decisions in your personal and professional life. Remember to utilize different methods to cross-check your answers and always focus on understanding the context of the problem to effectively apply the appropriate formula. With practice and consistent application, you'll develop a strong grasp of percentages and their practical implications.
Latest Posts
Latest Posts
-
What Is The Gcf Of 24 And 42
May 14, 2025
-
How Old Is Someone Born In 68
May 14, 2025
-
Cuanto Falta Para El 4 De Agosto
May 14, 2025
-
28 Cups Equals How Many Quarts
May 14, 2025
-
2 5 X 10 24 Molecules To Moles
May 14, 2025
Related Post
Thank you for visiting our website which covers about 25 Is 60 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.