3 1/4 Divided By 3 As A Fraction
Treneri
May 11, 2025 · 5 min read
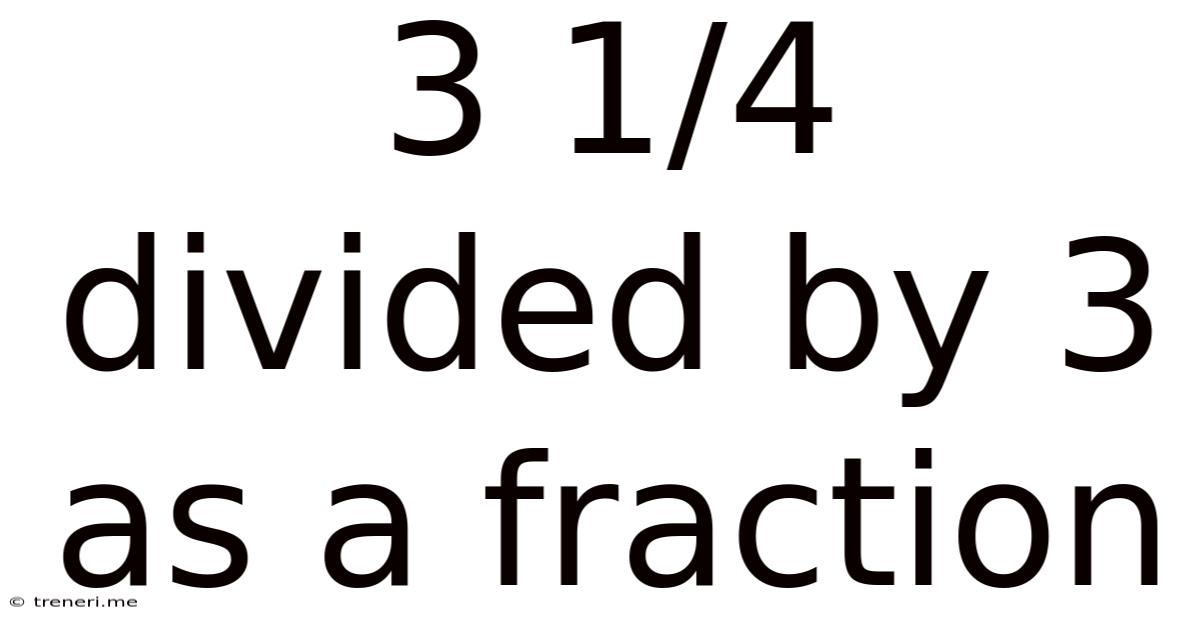
Table of Contents
3 1/4 Divided by 3 as a Fraction: A Comprehensive Guide
Dividing mixed numbers can seem daunting, but with a systematic approach, it becomes straightforward. This comprehensive guide will walk you through the process of dividing 3 1/4 by 3, explaining the steps clearly and providing additional examples to solidify your understanding. We'll explore different methods, address common pitfalls, and even delve into the practical applications of such calculations.
Understanding Mixed Numbers and Improper Fractions
Before diving into the division, let's refresh our understanding of mixed numbers and improper fractions. A mixed number combines a whole number and a fraction, like 3 1/4. An improper fraction, on the other hand, has a numerator larger than or equal to its denominator, such as 13/4. These two representations are equivalent; they simply express the same quantity differently.
Converting between mixed numbers and improper fractions is crucial for performing division. To convert a mixed number to an improper fraction, we multiply the whole number by the denominator, add the numerator, and then place the result over the original denominator.
For 3 1/4:
(3 * 4) + 1 = 13
So, 3 1/4 is equivalent to 13/4.
Method 1: Converting to Improper Fraction and Dividing
This is arguably the most common and straightforward method. We'll convert the mixed number into an improper fraction, and then perform the division.
Step 1: Convert the mixed number to an improper fraction.
As shown above, 3 1/4 converts to 13/4.
Step 2: Rewrite the division problem as a multiplication problem.
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 3 (or 3/1) is 1/3. Therefore, our problem becomes:
13/4 * 1/3
Step 3: Multiply the numerators and denominators.
Multiply the numerators together (13 * 1 = 13) and the denominators together (4 * 3 = 12). This gives us:
13/12
Step 4: Simplify the fraction (if possible).
In this case, 13/12 is an improper fraction. We can convert it to a mixed number by dividing the numerator (13) by the denominator (12).
13 ÷ 12 = 1 with a remainder of 1.
Therefore, 13/12 simplifies to 1 1/12.
So, 3 1/4 divided by 3 is 1 1/12.
Method 2: Dividing the Whole Number and Fractional Parts Separately (Less Efficient but Illustrative)
While less efficient for this specific problem, understanding this method helps illustrate the underlying principles of division with mixed numbers. We can divide the whole number part and the fractional part separately, then combine the results. However, this approach requires careful consideration of remainders.
Step 1: Divide the whole number part.
Divide the whole number part of the mixed number (3) by the divisor (3):
3 ÷ 3 = 1
Step 2: Divide the fractional part.
Divide the fractional part (1/4) by the divisor (3):
(1/4) ÷ 3 = 1/4 * 1/3 = 1/12
Step 3: Combine the results.
Add the results from steps 1 and 2:
1 + 1/12 = 1 1/12
This method yields the same answer as the first method, demonstrating the consistency of the approach. However, it’s generally more cumbersome and prone to errors, especially with more complex mixed numbers.
Practical Applications and Real-World Examples
Understanding the division of mixed numbers is crucial in various real-world scenarios. Here are a few examples:
-
Cooking: If a recipe calls for 3 1/4 cups of flour and you want to make a third of the recipe, you'd need to calculate (3 1/4) ÷ 3 = 1 1/12 cups of flour.
-
Construction: Imagine you have a board that is 3 1/4 feet long and need to cut it into 3 equal pieces. Each piece would be 1 1/12 feet long.
-
Sewing: If you have 3 1/4 yards of fabric and need to cut it into 3 equal pieces for a project, each piece would measure 1 1/12 yards.
-
Data Analysis: Let's say you have a dataset with an average value of 3 1/4 units and you want to divide it into 3 equal groups. Each group would have an average of 1 1/12 units.
Common Mistakes to Avoid
-
Forgetting to convert mixed numbers to improper fractions before dividing: This is the most common mistake. Dividing directly with the mixed number will usually lead to an incorrect result.
-
Incorrectly finding the reciprocal: Remember that to divide by a fraction, you multiply by its reciprocal (flip the numerator and denominator).
-
Not simplifying the final answer: Always simplify your answer to its lowest terms.
Further Practice and Advanced Concepts
To solidify your understanding, practice dividing various mixed numbers by different divisors. You can create your own practice problems or find exercises online. As you become more comfortable, you can explore more advanced concepts such as dividing mixed numbers by mixed numbers or incorporating negative numbers.
Conclusion
Dividing 3 1/4 by 3, resulting in 1 1/12, is a fundamental skill with practical applications across various fields. By understanding the steps involved in converting mixed numbers to improper fractions, applying the rules of fraction division, and simplifying the final answer, you can confidently tackle similar calculations. Remember to avoid common mistakes and practice regularly to master this essential mathematical skill. This comprehensive guide equipped you with the knowledge and tools to solve these problems efficiently and accurately. The ability to work confidently with fractions is a valuable asset in numerous aspects of life, from everyday tasks to more complex professional scenarios.
Latest Posts
Latest Posts
-
Whats The Square Root Of 1 9
May 12, 2025
-
What Is 1 2 As An Improper Fraction
May 12, 2025
-
2 7 Kg To Lbs And Oz
May 12, 2025
-
How Many Days Is 39 Years
May 12, 2025
-
How Many Square Feet In One Bundle Of Roofing Shingles
May 12, 2025
Related Post
Thank you for visiting our website which covers about 3 1/4 Divided By 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.