What's The Square Root Of 1/9
Treneri
May 12, 2025 · 4 min read
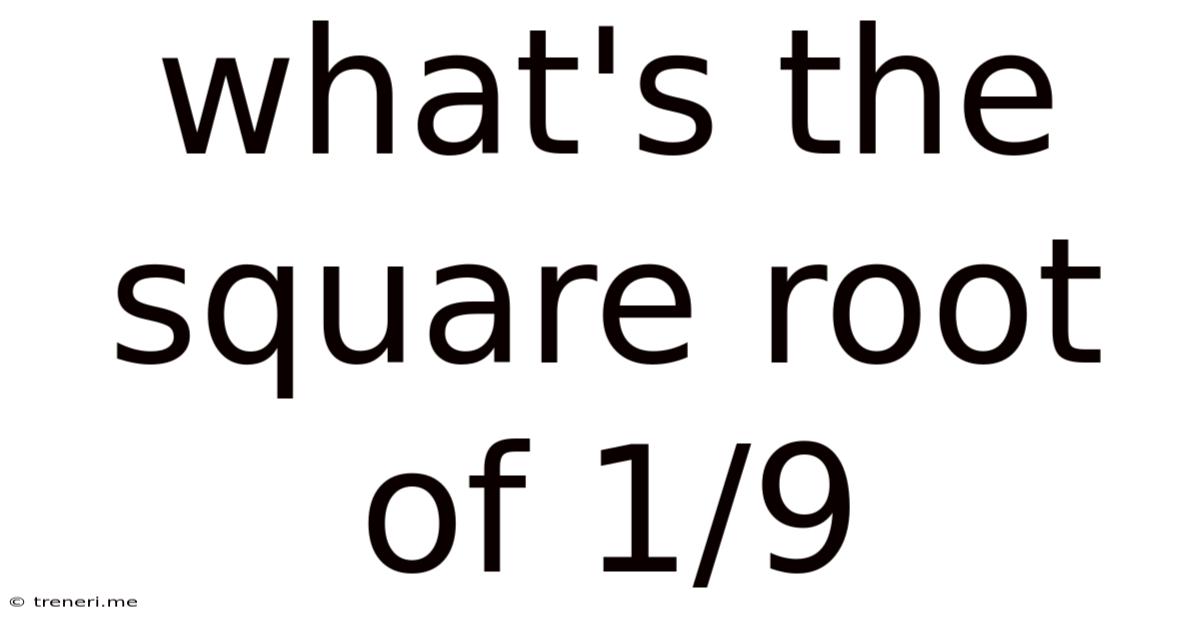
Table of Contents
What's the Square Root of 1/9? A Deep Dive into Square Roots and Fractions
The question, "What's the square root of 1/9?" might seem deceptively simple at first glance. However, understanding its solution unlocks a deeper understanding of fundamental mathematical concepts, particularly concerning square roots and fractions. This article will not only answer the question directly but will also explore the underlying principles involved, providing a comprehensive guide for anyone looking to strengthen their mathematical foundation.
Understanding Square Roots
Before diving into the specifics of the square root of 1/9, let's refresh our understanding of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9. Similarly, the square root of 16 (√16) is 4 because 4 * 4 = 16.
It's crucial to remember that every positive number has two square roots: a positive and a negative. While √9 = 3, it's equally true that (-3) * (-3) = 9. However, when we use the radical symbol (√), we typically refer to the principal square root, which is the non-negative square root.
Working with Fractions
Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). Understanding fraction operations is essential for solving problems involving the square root of fractions.
Simplifying Fractions
Before calculating the square root, it's often beneficial to simplify the fraction if possible. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. For example, the fraction 6/12 can be simplified to 1/2 by dividing both the numerator and denominator by 6 (their GCD).
Square Root of a Fraction
To find the square root of a fraction, we simply take the square root of the numerator and divide it by the square root of the denominator. This can be expressed as:
√(a/b) = √a / √b
This formula holds true as long as both 'a' and 'b' are non-negative.
Calculating the Square Root of 1/9
Now, let's apply our knowledge to find the square root of 1/9.
Using the formula for the square root of a fraction:
√(1/9) = √1 / √9
We know that:
- √1 = 1 (because 1 * 1 = 1)
- √9 = 3 (because 3 * 3 = 9)
Therefore:
√(1/9) = 1/3
The principal square root of 1/9 is 1/3. This is because (1/3) * (1/3) = 1/9. The other square root is -1/3, since (-1/3) * (-1/3) also equals 1/9.
Further Exploration: Square Roots and Different Number Systems
The concept of square roots extends beyond simple fractions and whole numbers. Let's explore its application in other number systems:
Decimal Numbers
The square root of a decimal number can be calculated using similar principles. For example, to find the square root of 0.25, we can convert it to a fraction (1/4) and then calculate the square root:
√0.25 = √(1/4) = √1 / √4 = 1/2 = 0.5
Irrational Numbers
Some numbers don't have exact fractional or decimal representations. These are called irrational numbers. A classic example is the square root of 2 (√2), which is approximately 1.414. Irrational numbers have infinite, non-repeating decimal expansions.
Complex Numbers
The concept of square roots also extends into the realm of complex numbers. A complex number has a real part and an imaginary part (involving the imaginary unit 'i', where i² = -1). For example, the square root of -1 is 'i'.
Practical Applications of Square Roots
Square roots appear frequently in various fields:
- Geometry: Calculating the diagonal of a square or the hypotenuse of a right-angled triangle using the Pythagorean theorem involves square roots.
- Physics: Many physics formulas, particularly in mechanics and wave phenomena, incorporate square roots.
- Engineering: Structural engineering, electrical engineering, and many other branches heavily utilize square roots in their calculations.
- Computer Graphics: Square roots are essential in 3D graphics for distance calculations and transformations.
- Statistics: Standard deviation calculations in statistics use square roots.
Mastering Square Roots: Tips and Tricks
- Memorize Perfect Squares: Familiarizing yourself with the squares of small integers (1, 4, 9, 16, 25, etc.) will greatly speed up your calculations.
- Prime Factorization: Breaking down numbers into their prime factors can simplify the process of finding square roots, particularly for larger numbers.
- Use a Calculator: For complex or large numbers, using a calculator is efficient and accurate.
- Practice Regularly: The more you practice solving problems involving square roots, the more proficient you'll become.
Conclusion: Beyond the Basics of √(1/9)
While the initial question, "What's the square root of 1/9?", provided a simple starting point, exploring its solution has unveiled a wealth of knowledge about square roots, fractions, and their applications across various mathematical domains. Understanding these fundamentals builds a robust mathematical foundation, crucial for success in numerous academic and professional fields. The journey from a seemingly basic question to a comprehensive understanding of its underlying principles exemplifies the beauty and interconnectedness of mathematics. Remember to practice regularly, explore further applications, and continue to expand your mathematical knowledge. This deeper understanding will undoubtedly enhance your problem-solving skills and provide you with a strong base for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
How Long To Be In The Sun To Tan
May 12, 2025
-
What Is The Greatest Common Factor Of 72 And 40
May 12, 2025
-
What Fractions Are Equivalent To 6 10
May 12, 2025
-
What Are The Factors For 93
May 12, 2025
-
Convert Mg Per Litre To Ppm
May 12, 2025
Related Post
Thank you for visiting our website which covers about What's The Square Root Of 1/9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.