3 Root 2 Times 3 Root 2
Treneri
May 15, 2025 · 5 min read
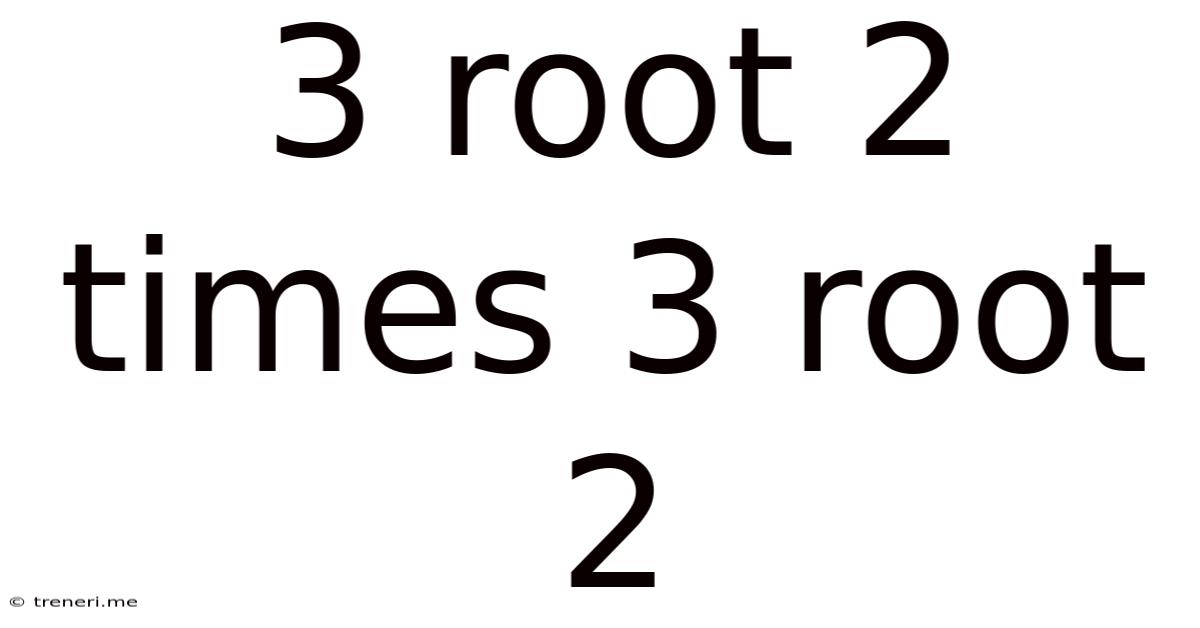
Table of Contents
3√2 x 3√2: A Deep Dive into Radical Multiplication and its Applications
The seemingly simple expression "3√2 x 3√2" offers a fascinating gateway into understanding the fundamental principles of radical multiplication and its broader applications in mathematics, science, and engineering. This article will explore this expression in detail, explaining the steps involved in its simplification, exploring related concepts, and demonstrating its relevance in various fields.
Understanding Radicals
Before delving into the calculation, let's establish a solid foundation in radical notation. A radical, symbolized by the radical symbol (√), represents a root of a number. The number inside the radical symbol is called the radicand. The small number placed above and to the left of the radical symbol, called the index, indicates the type of root. For example:
- √x: This represents the square root of x (index is implicitly 2).
- ∛x: This represents the cube root of x (index is 3).
- ⁿ√x: This represents the nth root of x (index is n).
In our expression, "3√2," we have a coefficient (3) multiplying a radical (√2). This means we have three instances of the square root of 2.
Calculating 3√2 x 3√2
Now, let's tackle the calculation: 3√2 x 3√2. The key to simplifying this expression lies in understanding that multiplication is commutative and associative. This means that the order of the numbers being multiplied does not affect the result, and we can group them in any way that simplifies the calculation.
We can rewrite the expression as:
(3 x 3) x (√2 x √2)
This simplification makes the calculation straightforward:
- 3 x 3 = 9
- √2 x √2 = 2 (The square root of a number multiplied by itself equals the number itself. √a x √a = a)
Therefore, the final result is:
9 x 2 = 18
Thus, 3√2 x 3√2 = 18
Extending the Concept: Generalizing Radical Multiplication
The principles used to solve 3√2 x 3√2 can be generalized to other radical expressions. Consider the following example:
a√b x c√d = ac√(bd)
This general formula highlights that:
- Coefficients multiply each other (a x c).
- Radicands (the numbers inside the square roots) multiply each other (b x d), remaining under the radical sign unless further simplification is possible.
This principle holds true for any type of root, not just square roots. For example:
2∛5 x 4∛3 = 8∛15
Applications in Various Fields
The seemingly simple multiplication of radicals finds surprising applications in various areas:
1. Geometry and Trigonometry
Radicals frequently appear in geometrical calculations, particularly when dealing with triangles. The Pythagorean theorem, a cornerstone of geometry, often leads to expressions involving square roots. For instance, calculating the length of the hypotenuse of a right-angled triangle with legs of length 3 and 4 involves the square root of 25 (√25 = 5). Expressions involving radicals become essential in calculating areas and volumes of irregular shapes.
2. Physics and Engineering
Many physical quantities and engineering calculations involve radicals. For example, the calculation of velocity, acceleration, and distance often involves square roots. In electrical engineering, impedance calculations frequently use complex numbers, which can include radicals. Furthermore, calculations involving oscillations and waves often lead to the use of trigonometric functions, which often involve radicals in their calculations.
3. Computer Graphics and Game Development
Radicals and their related concepts play a significant role in computer graphics and game development. For instance, calculations related to 3D modeling, animation, and physics engines frequently use vector mathematics which involves manipulations of coordinates and distances, leading to expressions with radicals.
4. Financial Modeling and Statistics
While not as direct as in physics or geometry, radicals can indirectly show up in financial modeling and statistical analysis. Statistical models often involve standard deviations and variances, calculated with square roots. Financial models might utilize stochastic processes that involve probability distributions, many of which use square roots or higher-order radicals in their formulas.
Advanced Concepts and Extensions
Understanding the simple multiplication of 3√2 x 3√2 provides a foundation for exploring more advanced concepts:
1. Rationalizing the Denominator
This technique is crucial when dealing with fractions involving radicals in the denominator. The goal is to eliminate the radical from the denominator to make the expression simpler and easier to work with. This usually involves multiplying both the numerator and denominator by a suitable radical expression.
2. Solving Radical Equations
Radical equations contain variables within radicals. Solving such equations often involves squaring or cubing both sides of the equation to eliminate the radical, leading to polynomial equations.
3. Complex Numbers
The square root of a negative number introduces the concept of imaginary numbers (represented by 'i', where i² = -1). Combining real and imaginary numbers results in complex numbers, which expand the scope of radical calculations significantly, finding applications in various branches of science and engineering.
4. Nth Roots and Higher-Order Radicals
Beyond square roots and cube roots, there exist nth roots, where n can be any positive integer. These higher-order radicals are fundamental in algebra and number theory and have applications in advanced mathematical concepts.
Conclusion
The seemingly simple calculation of 3√2 x 3√2 provides a stepping stone into a vast landscape of mathematical concepts. From its underlying principles of radical multiplication and simplification to its applications in various fields, this expression represents a fundamental building block in mathematics and its related sciences. Understanding its nuances opens the door to a deeper appreciation of the power and elegance of mathematics and its crucial role in shaping our world. The ability to manipulate radical expressions fluently is essential for success in many academic disciplines and professional fields. Continuous learning and practice are vital for mastering this crucial aspect of mathematics. The journey from a simple calculation to a comprehensive understanding of radicals is one that rewards those willing to delve deeper into the mathematical landscape.
Latest Posts
Latest Posts
-
1972 Al 2024 Cuantos Anos Son
May 15, 2025
-
How Long Was 17 Years Ago
May 15, 2025
-
26 Divided By 3 With Remainder
May 15, 2025
-
What Is 7 Of 1 Million
May 15, 2025
-
How Many Hours Until 7 Pm Today
May 15, 2025
Related Post
Thank you for visiting our website which covers about 3 Root 2 Times 3 Root 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.