4 5 Divided By 3 As A Fraction
Treneri
May 09, 2025 · 5 min read
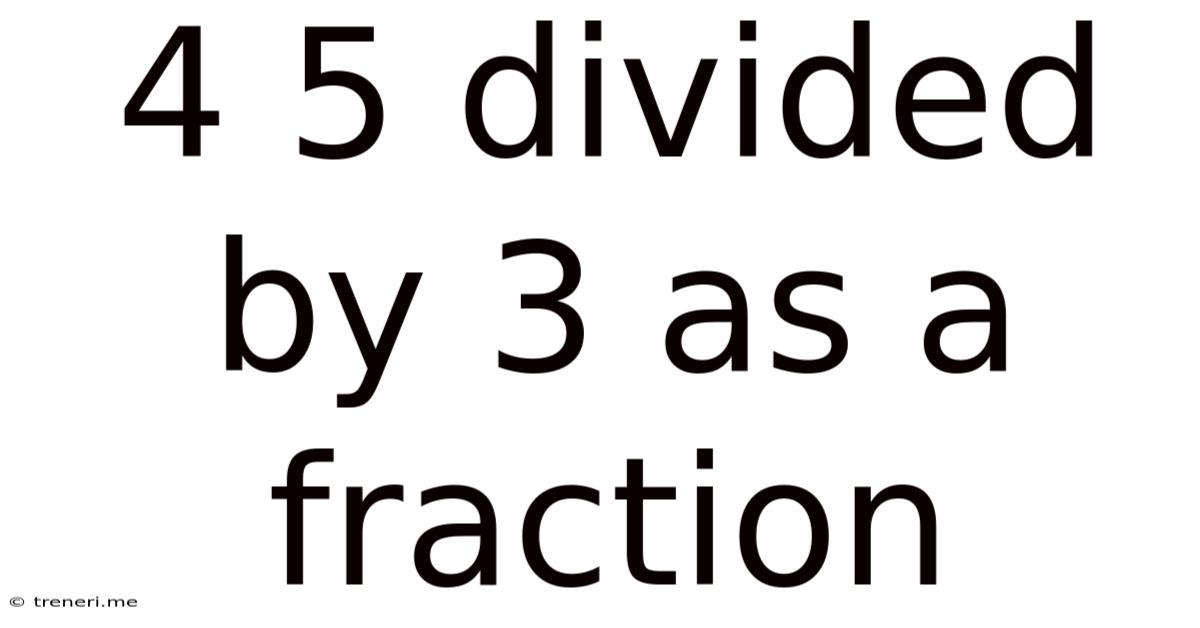
Table of Contents
4 5/3 as a Fraction: A Comprehensive Guide
Understanding fractions is fundamental to mathematics, and mastering their manipulation is crucial for success in various academic and practical scenarios. This article delves into the detailed process of converting the mixed number 4 5/3 into an improper fraction, exploring the underlying principles and providing a step-by-step guide. We'll also touch upon practical applications and offer tips for tackling similar problems.
Understanding Mixed Numbers and Improper Fractions
Before we dive into the conversion, let's clarify the terminology:
-
Mixed Number: A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). Our example, 4 5/3, is a mixed number. The whole number is 4, and the fraction is 5/3.
-
Improper Fraction: An improper fraction has a numerator that is greater than or equal to its denominator. The result of our conversion will be an improper fraction.
The key to converting a mixed number to an improper fraction lies in recognizing the relationship between the whole number and the fractional part. The whole number represents a certain number of whole units, while the fraction represents a part of a whole unit.
Converting 4 5/3 to an Improper Fraction: A Step-by-Step Guide
The conversion process involves two simple steps:
Step 1: Multiply the whole number by the denominator of the fraction.
In our example, the whole number is 4, and the denominator of the fraction 5/3 is 3. Therefore, we multiply 4 * 3 = 12.
Step 2: Add the result from Step 1 to the numerator of the fraction.
The result from Step 1 is 12, and the numerator of the fraction 5/3 is 5. Adding these together, we get 12 + 5 = 17.
Step 3: Keep the same denominator.
The denominator of the original fraction remains unchanged. Therefore, the denominator of our improper fraction is 3.
Putting it all together:
By combining the results from Steps 2 and 3, we get the improper fraction: 17/3. This means that 4 5/3 is equivalent to 17/3.
Verification and Understanding the Result
To verify our result, we can convert the improper fraction 17/3 back into a mixed number. We do this by performing division:
17 ÷ 3 = 5 with a remainder of 2.
The quotient (5) becomes the whole number, and the remainder (2) becomes the numerator of the fraction, while the divisor (3) remains the denominator. This gives us 5 2/3. Notice this isn't our original mixed number. This discrepancy highlights the importance of the initial fraction being simplified.
Since our original fraction, 5/3 is an improper fraction itself (the numerator is larger than the denominator), we should simplify it first.
5/3 can be expressed as 1 2/3.
Therefore, 4 5/3 is actually 4 + 1 2/3 = 5 2/3. Then, converting 5 2/3 to an improper fraction: (5 x 3) + 2 = 17, keeping the denominator 3, gives us 17/3. This confirms our initial calculation.
Practical Applications of Fraction Conversion
The ability to convert between mixed numbers and improper fractions is essential in many areas:
-
Baking and Cooking: Recipes often use fractions, and converting between mixed numbers and improper fractions is crucial for accurate measurements.
-
Construction and Engineering: Precise measurements and calculations are paramount in these fields, and fraction conversion ensures accuracy.
-
Finance: Calculating interest, proportions, and other financial metrics often involves working with fractions.
-
Data Analysis: Representing data and performing calculations on datasets frequently requires manipulating fractions.
-
Advanced Mathematics: Algebra, calculus, and other advanced mathematical fields rely heavily on a strong understanding of fractions and their manipulations.
Further Exploration and Related Concepts
Beyond the basic conversion, we can explore related concepts:
-
Simplifying Fractions: Once you've converted a mixed number to an improper fraction, it's often beneficial to simplify the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by the GCD. For example, 12/18 can be simplified to 2/3 by dividing both the numerator and the denominator by 6 (the GCD of 12 and 18).
-
Adding and Subtracting Fractions: Understanding improper fractions is crucial for performing addition and subtraction of fractions with different denominators. Converting to a common denominator is often necessary.
-
Multiplying and Dividing Fractions: While converting to improper fractions isn't always strictly necessary, it can often simplify the process, especially when dealing with mixed numbers.
-
Decimal Representation: Improper fractions can easily be converted into decimal representation by performing long division. This provides an alternative way to represent the same value.
Tips and Tricks for Mastering Fraction Conversion
-
Practice Regularly: The more you practice converting mixed numbers to improper fractions (and vice versa), the more comfortable and proficient you will become.
-
Use Visual Aids: Diagrams and visual representations can help you understand the concepts more intuitively.
-
Break Down Complex Problems: If you're dealing with a complex problem, break it down into smaller, more manageable steps.
-
Check Your Work: Always check your work to ensure accuracy. Converting back to a mixed number is a good way to verify your result.
-
Utilize Online Resources: Many online resources offer practice problems and tutorials to help you improve your skills.
Conclusion: The Importance of Understanding Fractions
Mastering the conversion of mixed numbers to improper fractions is a crucial skill in mathematics and has numerous practical applications in various fields. By understanding the underlying principles, practicing regularly, and utilizing helpful resources, you can build a strong foundation in this fundamental aspect of mathematics. This ability will not only improve your problem-solving skills but also enhance your overall mathematical proficiency. The conversion of 4 5/3 to 17/3, while seemingly simple, demonstrates a crucial building block in understanding more complex mathematical concepts. Therefore, solidifying this foundational knowledge is vital for future success in any field that utilizes numerical analysis.
Latest Posts
Latest Posts
-
What Is 25 Percent Off 75 Dollars
May 09, 2025
-
Is 2 A Factor Of 34
May 09, 2025
-
30 Days From Oct 3 2024
May 09, 2025
-
How Do I Measure The Size Of My Bike
May 09, 2025
-
60 Days From June 11 2024
May 09, 2025
Related Post
Thank you for visiting our website which covers about 4 5 Divided By 3 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.