4/7 + 3/5 As A Fraction
Treneri
May 14, 2025 · 6 min read
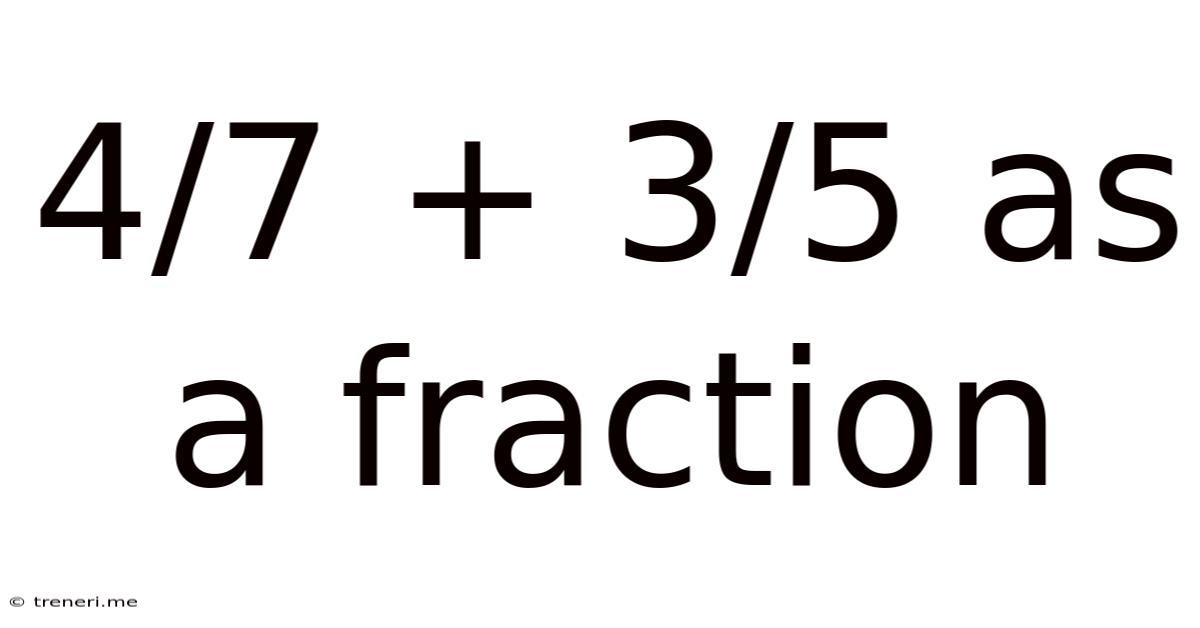
Table of Contents
4/7 + 3/5 as a Fraction: A Comprehensive Guide to Adding Fractions
Adding fractions might seem like a simple arithmetic task, but mastering the process is crucial for various mathematical applications. This comprehensive guide delves into the detailed steps and underlying principles of adding 4/7 and 3/5, explaining the process in a way that's easy to understand and remember. We'll explore the concept of finding the least common denominator (LCD), simplifying fractions, and checking our work for accuracy. We'll also delve into practical applications and explore similar problems to solidify your understanding.
Understanding the Basics of Fraction Addition
Before diving into the specific problem of adding 4/7 and 3/5, let's review the fundamental concepts of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number of a fraction, indicating the number of parts being considered.
- Denominator: The bottom number of a fraction, indicating the total number of equal parts the whole is divided into.
Adding fractions with different denominators requires a crucial step: finding a common denominator. This is because you can only add or subtract fractions when they share the same denominator. This common denominator represents the equal-sized pieces you're working with, ensuring consistent units for addition.
Finding the Least Common Denominator (LCD)
The least common denominator (LCD) is the smallest number that is a multiple of both denominators. Finding the LCD is essential for simplifying the addition process and obtaining the most reduced form of the resulting fraction. There are several methods to determine the LCD:
1. Listing Multiples: List the multiples of each denominator until you find the smallest common multiple.
Multiples of 7: 7, 14, 21, 28, 35, 42… Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40…
The smallest common multiple is 35. Therefore, the LCD of 7 and 5 is 35.
2. Prime Factorization: Break down each denominator into its prime factors. The LCD is the product of the highest powers of all prime factors present in either denominator.
7 = 7 (7 is a prime number) 5 = 5 (5 is a prime number)
LCD = 7 x 5 = 35
Converting Fractions to a Common Denominator
Once the LCD is found (which is 35 in this case), the next step is to convert both fractions to equivalent fractions with the LCD as their denominator. This is done by multiplying both the numerator and the denominator of each fraction by the appropriate factor.
For 4/7: To change the denominator from 7 to 35, we multiply by 5 (because 7 x 5 = 35). We must also multiply the numerator by 5 to maintain the fraction's value.
(4/7) x (5/5) = 20/35
For 3/5: To change the denominator from 5 to 35, we multiply by 7 (because 5 x 7 = 35). Again, we multiply the numerator by 7 as well.
(3/5) x (7/7) = 21/35
Adding the Fractions
Now that both fractions have the same denominator (35), we can add the numerators directly:
20/35 + 21/35 = (20 + 21) / 35 = 41/35
Simplifying the Resulting Fraction
The resulting fraction, 41/35, is an improper fraction (where the numerator is greater than the denominator). To express this as a mixed number, we perform division:
41 ÷ 35 = 1 with a remainder of 6.
This means 41/35 can be written as 1 6/35. This is the simplest form of the fraction because the greatest common divisor (GCD) of 6 and 35 is 1. Therefore, it cannot be simplified further.
Step-by-Step Summary of 4/7 + 3/5
Let's summarize the entire process for clarity:
- Find the LCD: The LCD of 7 and 5 is 35.
- Convert to Common Denominator:
- 4/7 becomes 20/35 (multiply numerator and denominator by 5)
- 3/5 becomes 21/35 (multiply numerator and denominator by 7)
- Add the Numerators: 20/35 + 21/35 = 41/35
- Simplify (if necessary): 41/35 simplifies to 1 6/35.
Therefore, 4/7 + 3/5 = 1 6/35
Practical Applications and Real-World Examples
Understanding fraction addition isn't just about solving math problems; it's a crucial skill applicable to various real-world situations:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Adding fractions is essential for accurately calculating the total amount of an ingredient needed. For instance, if a recipe calls for 2/3 cup of flour and 1/4 cup of sugar, you'd need to add these fractions to determine the total amount of dry ingredients.
-
Construction and Engineering: Precision is paramount in construction and engineering projects. Calculating lengths, areas, and volumes often involves adding fractions to ensure accuracy and avoid errors. For example, calculating the total length of a structure composed of several parts with fractional measurements requires adding fractions.
-
Finance and Budgeting: Dealing with finances often involves working with fractions or percentages (which are essentially fractions). Adding fractions helps in calculating total expenses, tracking budgets, or dividing shares.
-
Sewing and Tailoring: Sewing projects involve precise measurements. Adding fractions is essential for accurate calculations of fabric lengths and pattern adjustments.
-
Data Analysis and Statistics: Fractions and decimals are ubiquitous in data analysis and statistics. Adding fractions might be required to calculate average values or proportions within a dataset.
Similar Problems and Further Practice
To solidify your understanding of adding fractions, let's explore similar problems:
-
1/3 + 2/5: Find the LCD (15), convert the fractions (5/15 + 6/15), add the numerators (11/15). The result is already in its simplest form.
-
5/8 + 3/4: Find the LCD (8), convert the fractions (5/8 + 6/8), add the numerators (11/8), simplify to 1 3/8.
-
2/9 + 1/6: Find the LCD (18), convert the fractions (4/18 + 3/18), add the numerators (7/18).
Working through these problems will reinforce your understanding of the process and enhance your ability to solve more complex fraction addition problems.
Conclusion: Mastering Fraction Addition
Adding fractions, while seemingly basic, is a fundamental mathematical operation with broad applications. Understanding the steps involved—finding the LCD, converting fractions to a common denominator, adding the numerators, and simplifying the result—is crucial for solving various mathematical and real-world problems. Practice is key to mastering this skill, so work through the examples and similar problems to build confidence and accuracy. By understanding the principles behind fraction addition, you'll develop a strong foundation for tackling more advanced mathematical concepts. Remember, consistent practice and a solid understanding of the underlying concepts are the keys to success in mathematics.
Latest Posts
Latest Posts
-
How Old Is Someone Born In 68
May 14, 2025
-
Cuanto Falta Para El 4 De Agosto
May 14, 2025
-
28 Cups Equals How Many Quarts
May 14, 2025
-
2 5 X 10 24 Molecules To Moles
May 14, 2025
-
How To Find Are Of A Triangle
May 14, 2025
Related Post
Thank you for visiting our website which covers about 4/7 + 3/5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.