40 9 As A Mixed Number
Treneri
May 10, 2025 · 5 min read
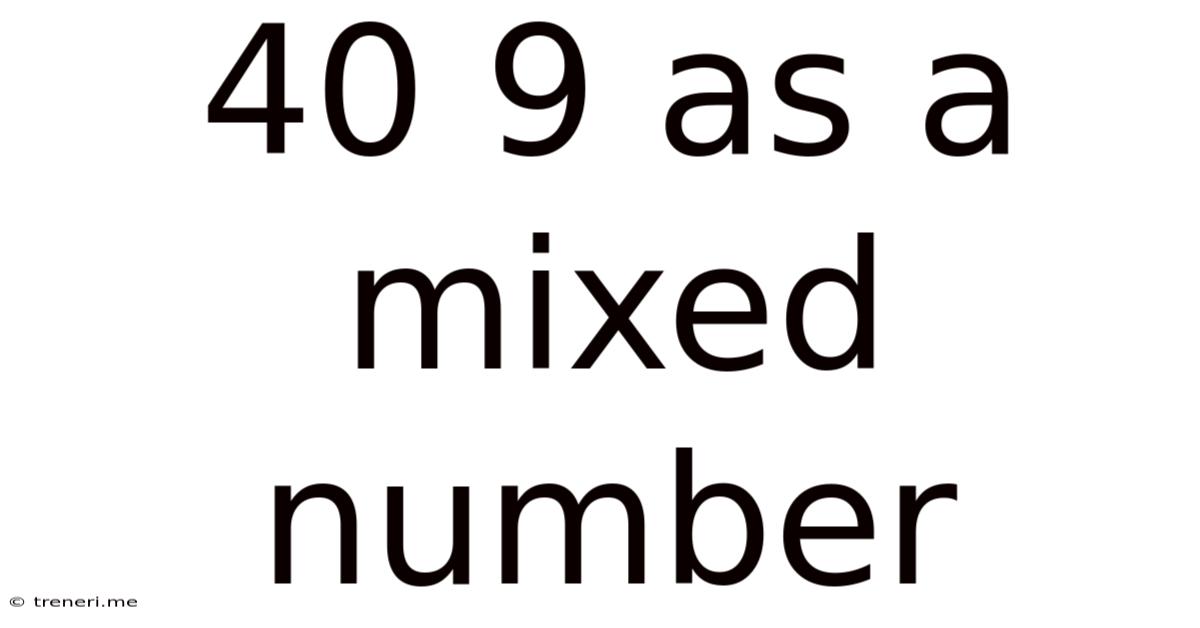
Table of Contents
40/9 as a Mixed Number: A Comprehensive Guide
Understanding fractions and their conversions is a fundamental skill in mathematics. This guide delves into the process of converting the improper fraction 40/9 into a mixed number, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll also explore the broader context of fractions and their applications.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number; 2 is the whole number, and ¾ is the proper fraction.
Conversely, an improper fraction has a numerator that is greater than or equal to the denominator. 40/9 is an improper fraction because 40 (the numerator) is larger than 9 (the denominator). Converting improper fractions to mixed numbers makes them easier to visualize and understand in many contexts.
Converting 40/9 to a Mixed Number: Step-by-Step
The process of converting an improper fraction to a mixed number involves division. Here's how to convert 40/9:
Step 1: Divide the Numerator by the Denominator
Divide the numerator (40) by the denominator (9):
40 ÷ 9 = 4 with a remainder of 4
Step 2: Identify the Whole Number and the Remainder
The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 4.
The remainder (the number left over after the division) becomes the numerator of the fractional part of the mixed number. The remainder is 4.
Step 3: Form the Mixed Number
The denominator of the fraction in the mixed number remains the same as the denominator of the original improper fraction. Therefore, the denominator is 9.
Combining the whole number and the fraction, we get the mixed number:
4 ⁴⁄₉
Understanding the Conversion: A Deeper Look
The conversion from 40/9 to 4 ⁴⁄₉ represents the same quantity. Imagine you have 40 identical objects, and you want to group them into sets of 9. You can form 4 complete sets of 9, with 4 objects remaining. This perfectly mirrors the result of our division: 4 complete sets (the whole number) and 4 objects left over (the remainder forming the fraction ⁴⁄₉).
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in various real-world scenarios:
-
Measurement: Measuring ingredients in a recipe, lengths of materials, or quantities of liquids often involves mixed numbers (e.g., 2 ½ cups of flour, 5 ¾ inches of ribbon).
-
Time: Telling time involves mixed numbers (e.g., 2:45 can be represented as 2 ¾ hours).
-
Data Analysis: Representing data involving parts of wholes often requires mixed numbers for better clarity and understanding.
-
Geometry: Calculating areas and volumes of shapes can result in mixed numbers.
-
Everyday Calculations: Many daily calculations, from dividing resources to solving problems, naturally lend themselves to mixed number representations.
Working with Mixed Numbers: Addition, Subtraction, Multiplication, and Division
Once you have converted an improper fraction to a mixed number, you can perform various mathematical operations. While adding and subtracting mixed numbers directly is possible, it's often easier to convert them back to improper fractions, perform the operation, and then convert the result back to a mixed number if needed.
Addition: To add mixed numbers, you can either add the whole numbers and the fractions separately, or convert both to improper fractions, add, and then convert back to a mixed number.
Subtraction: Similar to addition, you can either subtract the whole numbers and fractions separately or convert to improper fractions, subtract, and convert back.
Multiplication: To multiply mixed numbers, it's generally easier to convert them to improper fractions first, then multiply the numerators and denominators, and finally convert the result back to a mixed number if it's an improper fraction.
Division: To divide mixed numbers, convert them to improper fractions first, then invert the second fraction (reciprocal) and multiply. Convert the result back to a mixed number if necessary.
Simplifying Fractions: A Key Skill
In many cases, the fractional part of a mixed number can be simplified. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
For example, if you had the mixed number 6 ⁶⁄₁₂, you would simplify the fraction ⁶⁄₁₂ by dividing both the numerator and denominator by 6, resulting in ½. The simplified mixed number would be 6 ½.
Other Conversions Involving Fractions
Besides converting improper fractions to mixed numbers, it's also useful to know how to convert:
-
Mixed numbers to improper fractions: To do this, multiply the whole number by the denominator, add the numerator, and keep the same denominator. For example, 3 ¼ becomes (3 * 4 + 1)/4 = 13/4.
-
Decimals to fractions: This involves writing the decimal as a fraction with a denominator that is a power of 10 (10, 100, 1000, etc.), and then simplifying the fraction.
-
Fractions to decimals: This involves dividing the numerator by the denominator.
Mastering these conversions enhances your overall understanding of fractions and their applications.
Real-World Examples Using Mixed Numbers
Let's illustrate the practical use of mixed numbers with a few scenarios:
Scenario 1: Baking a Cake
A cake recipe calls for 2 ⅓ cups of flour and 1 ¼ cups of sugar. To determine the total amount of dry ingredients, you would add the mixed numbers: 2 ⅓ + 1 ¼ = 3 ⁷⁄₁₂ cups.
Scenario 2: Measuring Lumber
You need to cut a piece of lumber that measures 5 ⅝ inches. This mixed number accurately represents the required length.
Scenario 3: Calculating Travel Time
A journey takes 3 hours and 20 minutes. This can be expressed as 3 ⅓ hours, making it easier to perform calculations involving travel time.
Conclusion: Mastering Mixed Numbers for Mathematical Fluency
Converting 40/9 to the mixed number 4 ⁴⁄₉ is a fundamental skill in mathematics. Understanding this conversion, along with the ability to work with mixed numbers in various operations, is crucial for success in many areas, from everyday life to advanced mathematical concepts. By mastering the techniques outlined in this guide, you'll gain a deeper understanding of fractions and enhance your overall mathematical fluency. Remember to practice regularly to reinforce your understanding and build confidence in working with fractions and mixed numbers. The more you practice, the more intuitive these conversions will become.
Latest Posts
Latest Posts
-
How Long To Read The Hobbit
May 10, 2025
-
How Do You Find The Area Of A Wall
May 10, 2025
-
9 Out Of 24 As A Percentage
May 10, 2025
-
Cuanto Es El 20 De 400
May 10, 2025
-
How Much Weight Can A Weld Hold
May 10, 2025
Related Post
Thank you for visiting our website which covers about 40 9 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.