40 Out Of 44 As A Percentage
Treneri
May 10, 2025 · 5 min read
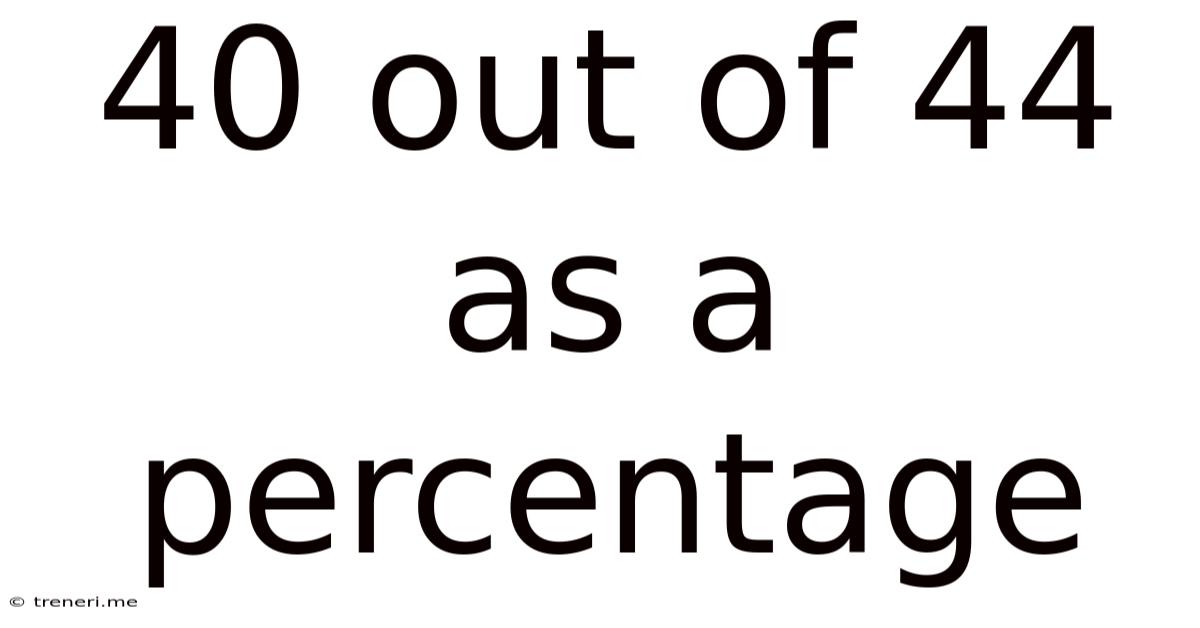
Table of Contents
40 out of 44 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill in various aspects of life, from academic pursuits to professional settings. Understanding how to determine percentages accurately is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will delve into the process of calculating 40 out of 44 as a percentage, explaining the method step-by-step and providing valuable insights into percentage calculations in general. We'll also explore various applications and explore related percentage problems.
Understanding Percentages
Before we dive into the specific calculation, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred," indicating a proportional relationship to the whole. For instance, 50% means 50 out of 100, or one-half. This representation provides a standardized and easily comparable way to express proportions.
Calculating 40 out of 44 as a Percentage
To calculate 40 out of 44 as a percentage, we follow a straightforward process:
Step 1: Express the values as a fraction.
We start by expressing the given values as a fraction: 40/44. This fraction represents the ratio of the part (40) to the whole (44).
Step 2: Convert the fraction to a decimal.
To convert the fraction to a decimal, we divide the numerator (40) by the denominator (44):
40 ÷ 44 ≈ 0.909
Step 3: Convert the decimal to a percentage.
To express the decimal as a percentage, we multiply it by 100 and add the "%" symbol:
0.909 × 100 ≈ 90.9%
Therefore, 40 out of 44 is approximately 90.9%.
Rounding Percentages
In many cases, percentage calculations result in decimals. The practice of rounding ensures that the percentage is presented in a clear and concise manner. The level of precision required depends on the context. For instance, in financial contexts, high precision is usually needed, while in general scenarios, rounding to one decimal place is often sufficient.
In our example, 90.9% is already rounded to one decimal place. If we needed to round to the nearest whole number, the result would be 91%.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous across many disciplines. Here are a few examples:
-
Academic Performance: Calculating grades, based on scores obtained in exams and assignments. For instance, if a student scores 35 out of 40 in a test, the percentage score is (35/40) * 100 = 87.5%.
-
Financial Matters: Calculating interest rates, discounts, taxes, and profit margins. Understanding percentage changes in investment values is crucial for financial planning.
-
Data Analysis: Representing data visually using pie charts and bar graphs, where percentages are often used to show proportions of different categories.
-
Scientific Studies: Expressing experimental results and statistical significance using percentages.
-
Everyday Life: Calculating tips in restaurants, understanding sale discounts, and comparing prices.
Advanced Percentage Calculations
Beyond simple calculations like 40 out of 44, various other percentage problems require more advanced approaches. Here are a few examples:
-
Percentage Increase/Decrease: Calculating the percentage change between two values. For example, if a price increases from $50 to $60, the percentage increase is ((60-50)/50) * 100 = 20%.
-
Finding a Percentage of a Number: Determining a specific percentage of a given number. For instance, finding 25% of 80: (25/100) * 80 = 20.
-
Finding the Original Value: Determining the original value after a percentage change is applied. For example, if a price is reduced by 10% to $90, the original price was $90 / (1 - 0.10) = $100.
Tips for Accurate Percentage Calculations
-
Double-check your work: Carefully review your calculations to avoid errors. Using a calculator can help, but always verify the results.
-
Understand the context: Pay close attention to the problem's specifics to correctly identify the part and the whole.
-
Use appropriate rounding: Round your final answer to a suitable level of precision depending on the context.
-
Practice regularly: Consistent practice enhances your understanding and proficiency in percentage calculations.
Solving Related Percentage Problems
Let's explore a few related percentage problems to solidify our understanding:
Problem 1: A student answers 38 out of 50 questions correctly on a test. What is their percentage score?
Solution:
-
Express as a fraction: 38/50
-
Convert to decimal: 38 ÷ 50 = 0.76
-
Convert to percentage: 0.76 × 100 = 76%
The student achieved a 76% score.
Problem 2: A shop offers a 15% discount on an item priced at $120. What is the final price after the discount?
Solution:
-
Calculate the discount amount: 15% of $120 = (15/100) × $120 = $18
-
Subtract the discount from the original price: $120 - $18 = $102
The final price after the discount is $102.
Problem 3: If a value increases from 150 to 180, what is the percentage increase?
Solution:
-
Find the difference: 180 - 150 = 30
-
Divide the difference by the original value: 30 ÷ 150 = 0.2
-
Convert to percentage: 0.2 × 100 = 20%
The percentage increase is 20%.
Conclusion
Calculating percentages is a valuable skill with numerous practical applications. Understanding the fundamental steps involved, such as converting fractions to decimals and decimals to percentages, is crucial for accurately determining percentages in various contexts. Through consistent practice and application, you can master this essential skill and confidently tackle diverse percentage-related problems. Remember to always double-check your work and round appropriately based on the context of the problem. With this knowledge, you'll be well-equipped to handle percentage calculations in your academic, professional, and personal life.
Latest Posts
Latest Posts
-
Crown Rump Length Chart In Mm
May 10, 2025
-
What Percentage Of 11 Is 4
May 10, 2025
-
1994 Was How Many Years Ago
May 10, 2025
-
3 Hours 30 Minutes Marathon Pace
May 10, 2025
-
How Many Square Feet Is 20 X 30
May 10, 2025
Related Post
Thank you for visiting our website which covers about 40 Out Of 44 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.