50 Of 250 Is What Percent
Treneri
May 12, 2025 · 5 min read
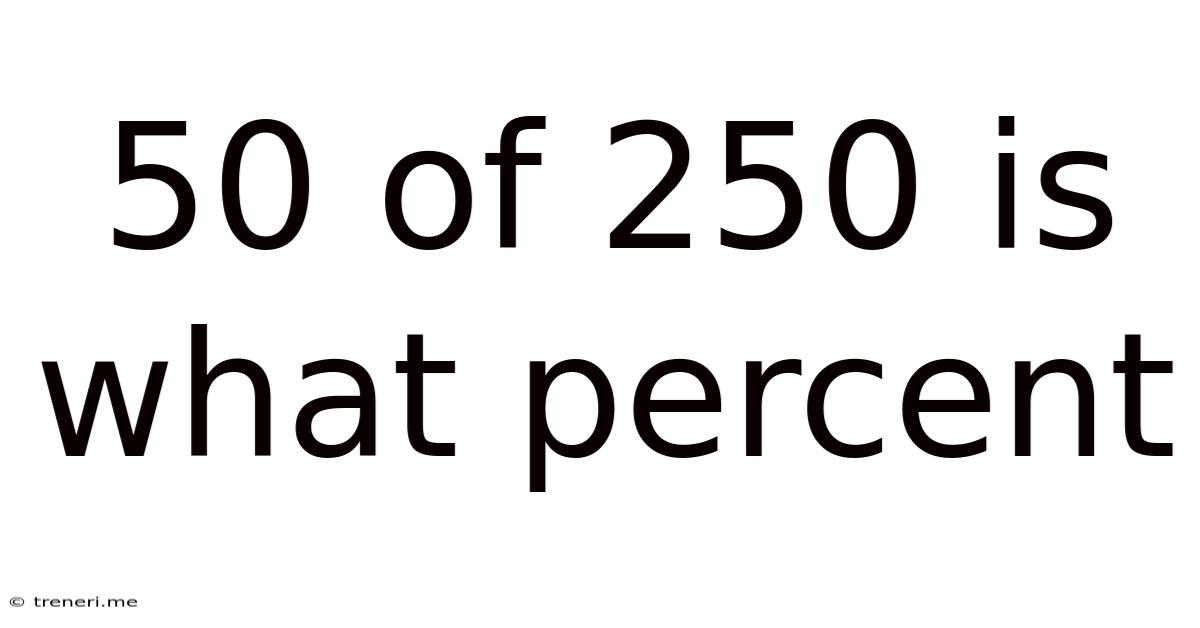
Table of Contents
50 out of 250 is What Percent? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday budgeting and shopping to complex scientific analyses and business decisions. Understanding how to determine percentages accurately is crucial for making informed choices and interpreting data effectively. This comprehensive guide will delve into the calculation of "50 out of 250 is what percent?", exploring the underlying principles, providing step-by-step solutions, and offering various approaches to tackle similar percentage problems. We'll also discuss practical applications and explore the broader context of percentage calculations within mathematics and real-world scenarios.
Understanding Percentages
Before we dive into the specific calculation of 50 out of 250, let's establish a solid understanding of what percentages represent. A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" – it indicates the proportion of a quantity relative to a whole, which is considered to be 100%.
For instance, 50% means 50 out of 100, which can also be represented as the fraction 50/100 or the decimal 0.5. This simplifies the representation of proportions, making it easier to compare and understand different quantities relative to a common standard.
Calculating "50 out of 250 is What Percent?"
There are several ways to calculate what percentage 50 represents of 250. Let's explore the most common methods:
Method 1: Using the Fraction Method
This is a straightforward approach. We can express the problem as a fraction: 50/250. To convert this fraction into a percentage, we need to make the denominator (the bottom number) equal to 100.
-
Simplify the Fraction: We can simplify 50/250 by dividing both the numerator (top number) and the denominator by their greatest common divisor, which is 50. This simplifies the fraction to 1/5.
-
Convert to a Percentage: To convert the fraction 1/5 to a percentage, we need to find an equivalent fraction with a denominator of 100. We can achieve this by multiplying both the numerator and the denominator by 20: (1 * 20) / (5 * 20) = 20/100.
-
Express as a Percentage: Since 20/100 represents 20 out of 100, the percentage is 20%. Therefore, 50 out of 250 is 20%.
Method 2: Using the Decimal Method
This method involves converting the fraction to a decimal and then multiplying by 100.
-
Convert to a Decimal: Divide the numerator (50) by the denominator (250): 50 ÷ 250 = 0.2
-
Multiply by 100: To express the decimal as a percentage, multiply it by 100: 0.2 * 100 = 20
-
Express as a Percentage: The result is 20%.
Method 3: Using the Percentage Formula
The basic percentage formula is: (Part / Whole) * 100 = Percentage
In this case:
- Part = 50
- Whole = 250
-
Substitute the Values: (50 / 250) * 100 = Percentage
-
Calculate the Result: (0.2) * 100 = 20
-
Express as a Percentage: The result is 20%.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a multitude of real-world situations. Here are some examples:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all involve percentage calculations. Understanding these percentages is crucial for making sound financial decisions. For example, if a store offers a 25% discount on an item, you can use percentage calculations to determine the final price.
-
Shopping: Comparing prices, evaluating discounts, and understanding sales tax require proficiency in percentage calculations. Being able to quickly determine the best deal amongst various options saves money and enhances purchasing power.
-
Science and Statistics: Percentages are frequently used in data analysis, statistical modeling, and scientific research to represent proportions, probabilities, and variations within datasets. The ability to interpret and analyze percentage-based data is essential for scientific advancement.
-
Education: Grade calculations, test scores, and progress reports often rely on percentage representation. Understanding percentage scores is key to evaluating academic performance.
-
Business: Profit margins, market share analysis, sales growth, and expense tracking all rely heavily on percentage calculations. Successful business management and strategic decision-making depend on accurate percentage analysis.
Beyond the Basics: Advanced Percentage Calculations
While calculating "50 out of 250" is a relatively simple problem, the principles involved extend to more complex scenarios. Here are some advanced concepts related to percentage calculations:
-
Calculating the Whole: If you know the percentage and the part, you can calculate the whole using a modified version of the percentage formula: Whole = (Part / Percentage) * 100
-
Calculating the Part: If you know the percentage and the whole, you can calculate the part using another variation of the formula: Part = (Percentage / 100) * Whole
-
Percentage Increase/Decrease: Calculating percentage changes involves comparing an initial value to a final value. The formula for percentage increase is: [(Final Value - Initial Value) / Initial Value] * 100. The formula for percentage decrease is similar, but the difference is subtracted from the initial value.
-
Compound Interest: Compound interest calculations involve repeatedly applying percentage increases over time. This concept is crucial in understanding investment growth and loan repayments.
Troubleshooting Common Mistakes
Even seemingly straightforward percentage calculations can sometimes lead to errors. Here are some common mistakes to watch out for:
-
Incorrect Order of Operations: Always follow the order of operations (PEMDAS/BODMAS) when performing calculations to avoid errors.
-
Misinterpreting the Question: Carefully read and understand the problem statement before attempting to solve it. Make sure you correctly identify the 'part' and the 'whole'.
-
Incorrect Decimal Placement: Ensure you correctly place the decimal point when converting decimals to percentages and vice-versa.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple steps in a calculation. Round to an appropriate number of decimal places to maintain accuracy.
Conclusion
Calculating percentages is a fundamental skill with broad applications across various disciplines. Understanding the different methods for calculating percentages, along with the practical applications and potential pitfalls, empowers you to confidently tackle percentage-related problems in your daily life, academic pursuits, and professional endeavors. The seemingly simple calculation of "50 out of 250 is what percent?" serves as an excellent foundation for mastering the broader world of percentage calculations and their vast implications. By mastering these techniques, you enhance your ability to analyze data, interpret information, and make informed decisions in a multitude of contexts.
Latest Posts
Latest Posts
-
What Is The Gcf Of 27 And 72
May 13, 2025
-
What Percentage Of 10 Is 2
May 13, 2025
-
What Is The Quotient Of Es031 1 Jpg
May 13, 2025
-
Greatest Common Factor Of 36 And 33
May 13, 2025
-
Cuanto Es 3 Oz En Ml
May 13, 2025
Related Post
Thank you for visiting our website which covers about 50 Of 250 Is What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.