60 Is What Percent Of 90
Treneri
May 12, 2025 · 4 min read
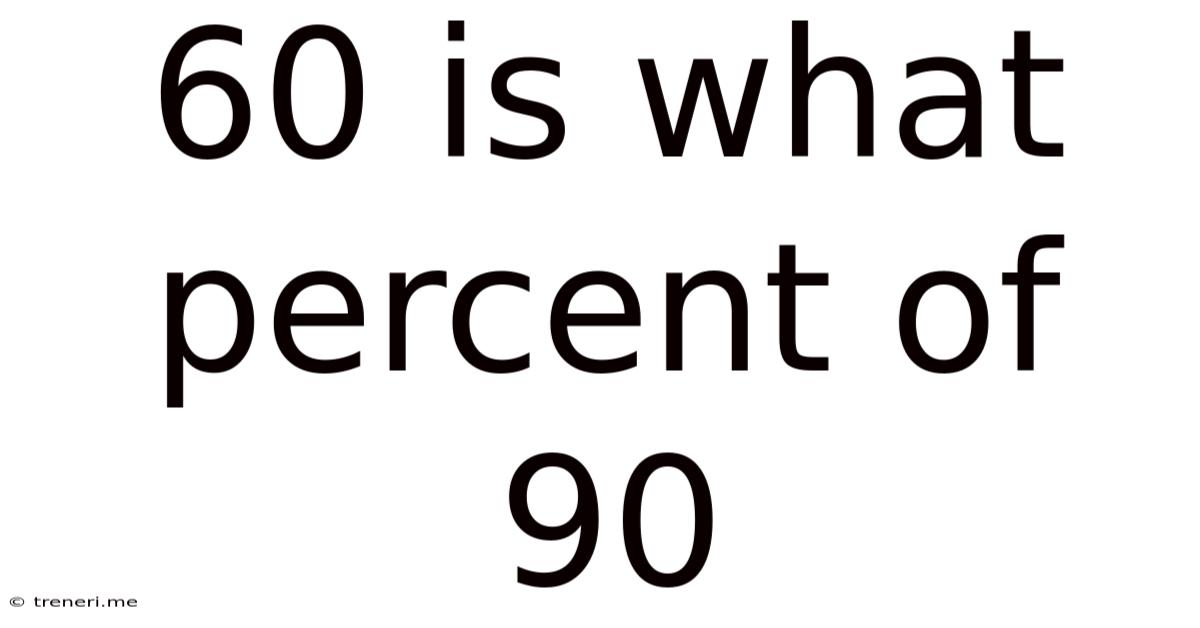
Table of Contents
60 is What Percent of 90: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill with wide-ranging applications in everyday life, from calculating discounts and tips to analyzing data and understanding financial reports. This article will delve deep into the question, "60 is what percent of 90?", providing a step-by-step solution, exploring the underlying concepts, and offering practical examples to solidify your understanding. We'll also explore related percentage calculations and how to solve similar problems efficiently.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of 100" (from the Latin per centum). Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Understanding this fundamental concept is key to solving percentage problems. We often use percentages to represent proportions, rates, and changes. For example:
- Discounts: A 20% discount on a $100 item means you save $20.
- Tax rates: A 6% sales tax means you pay an additional 6 cents for every dollar spent.
- Growth rates: A 5% increase in population means the population grew by 5 units for every 100 units.
Solving "60 is What Percent of 90?"
Now, let's tackle the specific problem: "60 is what percent of 90?". We can solve this using a simple formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 60 (the number we're comparing)
- Whole: 90 (the total number)
Let's plug the values into the formula:
(60 / 90) * 100% = Percentage
Simplifying the fraction:
(2/3) * 100% = Percentage
Now, perform the multiplication:
(2/3) * 100% ≈ 66.67%
Therefore, 60 is approximately 66.67% of 90.
Alternative Methods for Solving Percentage Problems
While the formula above is the most straightforward approach, there are alternative methods you can use, depending on your preference and the complexity of the problem:
Method 2: Using Proportions
You can set up a proportion to solve percentage problems. A proportion is an equation stating that two ratios are equal. In our case:
60/90 = x/100
Where 'x' represents the percentage we are trying to find. To solve for 'x', cross-multiply:
90x = 6000
x = 6000 / 90
x ≈ 66.67%
This method provides the same result as the previous one.
Method 3: Using Decimal Equivalents
You can convert the fraction (Part/Whole) into a decimal and then multiply by 100% to find the percentage.
60/90 = 0.6667
0.6667 * 100% ≈ 66.67%
Practical Applications and Real-World Examples
Percentage calculations are crucial in numerous real-world scenarios. Here are a few examples:
-
Calculating Sales Tax: If a product costs $50 and the sales tax is 8%, the tax amount is (8/100) * $50 = $4. The total cost is $50 + $4 = $54.
-
Determining Discounts: A store offers a 30% discount on a $150 item. The discount amount is (30/100) * $150 = $45. The final price is $150 - $45 = $105.
-
Analyzing Test Scores: If you scored 45 out of 60 on a test, your percentage score is (45/60) * 100% = 75%.
-
Understanding Financial Statements: Financial reports often use percentages to show profit margins, growth rates, and other key metrics.
Beyond the Basics: More Complex Percentage Problems
While the problem "60 is what percent of 90?" is relatively straightforward, percentage calculations can become more complex. Let's explore some variations:
-
Finding the Whole: If 25% of a number is 15, what is the number? This requires rearranging the formula: (Part/Percentage) * 100 = Whole. So, (15/25) * 100 = 60.
-
Finding the Part: What is 15% of 80? This involves a direct calculation: (15/100) * 80 = 12.
-
Percentage Increase/Decrease: A product's price increased from $50 to $60. What is the percentage increase? First, find the difference ($10), then divide by the original price ($50) and multiply by 100%: ($10/$50) * 100% = 20%.
Mastering Percentages: Tips and Tricks
Here are some helpful tips to improve your percentage calculation skills:
-
Practice Regularly: The more you practice, the more comfortable you'll become with the concepts and formulas.
-
Understand the Concepts: Don't just memorize formulas; understand the underlying logic behind them.
-
Use Calculators Wisely: Calculators can be helpful for complex calculations, but always try to understand the steps involved.
-
Break Down Complex Problems: Divide complex problems into smaller, more manageable parts.
-
Check Your Work: Always double-check your answers to ensure accuracy.
Conclusion
Understanding percentages is an essential life skill. This comprehensive guide has explored the solution to "60 is what percent of 90?", explained various methods for solving percentage problems, provided real-world examples, and offered tips for mastering these calculations. By applying these concepts and practicing regularly, you'll be able to confidently handle percentage calculations in any situation. Remember that mastering percentages isn't just about solving equations; it's about understanding the underlying relationships between numbers and their proportional representation. This understanding empowers you to interpret data, make informed decisions, and navigate the quantitative aspects of daily life with increased confidence and accuracy.
Latest Posts
Latest Posts
-
90 Days From September 29 2023
May 13, 2025
-
Given Each Pair Of Similar Triangles Find The Missing Value
May 13, 2025
-
6 Is What Percent Of 21
May 13, 2025
-
60 Days From June 27th 2024
May 13, 2025
-
Cuanto Es 400 Metros Cuadrados En Un Terreno
May 13, 2025
Related Post
Thank you for visiting our website which covers about 60 Is What Percent Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.