7 Out Of 40 As A Percentage
Treneri
May 10, 2025 · 5 min read
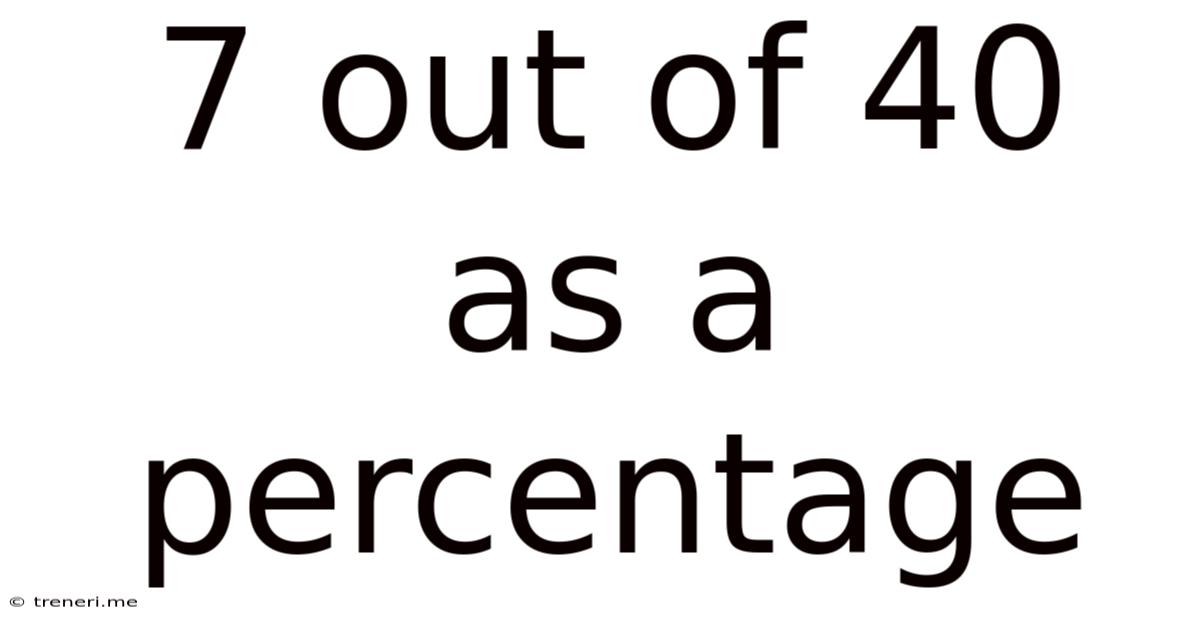
Table of Contents
7 out of 40 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in numerous aspects of life, from calculating discounts and taxes to interpreting data and statistics. Often, we encounter situations where we need to express a fraction as a percentage. This article delves into the specific calculation of "7 out of 40 as a percentage," providing a step-by-step guide, exploring different methods, and highlighting practical applications. We'll also examine related concepts to build a stronger understanding of percentage calculations.
Understanding the Concept of Percentage
A percentage is simply a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred." Therefore, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. When we calculate a percentage, we are determining the proportional value of one quantity relative to another, expressed as a fraction of 100.
Method 1: Using the Basic Formula
The most straightforward method to calculate 7 out of 40 as a percentage involves using the fundamental percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 7 (the number we are considering as a fraction of the whole)
- Whole: 40 (the total number)
Applying the formula:
(7 / 40) x 100% = 17.5%
Therefore, 7 out of 40 is 17.5%.
Method 2: Converting the Fraction to a Decimal
An alternative approach involves first converting the fraction 7/40 into a decimal, and then multiplying by 100%.
- Divide the part by the whole: 7 ÷ 40 = 0.175
- Multiply by 100%: 0.175 x 100% = 17.5%
This method yields the same result: 17.5%.
Method 3: Using Proportions
The concept of proportions can also be employed to solve this problem. We can set up a proportion where x represents the percentage we are trying to find:
7/40 = x/100
To solve for x, we cross-multiply:
40x = 700
x = 700 / 40
x = 17.5
Therefore, 7 out of 40 is 17.5%.
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is incredibly useful in various real-world scenarios. Here are a few examples:
1. Calculating Grades and Test Scores:
Imagine a student scored 7 out of 40 on a test. Knowing that this equates to 17.5% helps them understand their performance relative to the total possible score. This allows for better self-assessment and identification of areas needing improvement.
2. Determining Discounts and Sales:
Stores frequently advertise discounts as percentages. For example, a 17.5% discount on an item priced at $100 would result in a savings of $17.50. This calculation is crucial for consumers to determine the final price after a discount.
3. Analyzing Statistical Data:
In statistical analysis, percentages are commonly used to represent proportions within a larger dataset. For instance, if a survey of 40 people reveals that 7 prefer a particular brand, this translates to a 17.5% preference rate. This provides valuable insights into consumer preferences and market trends.
4. Calculating Interest Rates:
Understanding percentages is essential when dealing with interest rates on loans, savings accounts, and investments. Interest rates are typically expressed as percentages, allowing individuals to calculate the amount of interest earned or paid over a given period.
Expanding on Percentage Calculations: Related Concepts
To further enhance your understanding of percentage calculations, let's explore some related concepts:
1. Finding the Whole when Given the Percentage and Part:
Let's say you know that 17.5% of a certain number is 7. To find the whole, we can use the following formula:
Whole = (Part / Percentage) x 100
Substituting the known values:
Whole = (7 / 17.5) x 100 = 40
This confirms that 7 is indeed 17.5% of 40.
2. Calculating Percentage Increase or Decrease:
Percentage change is frequently used to compare values over time or between different categories. The formula for percentage increase or decrease is:
((New Value - Old Value) / Old Value) x 100%
A positive result indicates an increase, while a negative result signifies a decrease.
3. Working with Compound Percentages:
Compound percentages involve calculating percentages of percentages, which is common in scenarios such as compound interest. These calculations require a more iterative approach, often involving repeated applications of the percentage formula.
4. Understanding Percentage Points:
It's crucial to distinguish between percentage points and percentage change. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase. This distinction is essential for accurate interpretation of data.
Troubleshooting Common Percentage Calculation Errors
Several common mistakes can occur when working with percentages. Here are a few to watch out for:
- Incorrect Formula Application: Ensure you're using the correct formula for the specific calculation you're performing (e.g., finding the percentage, finding the part, finding the whole).
- Decimal Point Errors: Pay close attention to decimal points when converting fractions to decimals and performing calculations.
- Confusing Percentage Points and Percentage Change: Remember the distinction between these two concepts.
- Incorrect Rounding: When rounding percentages, follow established conventions to maintain accuracy.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a vital skill with broad applications across many areas of life. By understanding the fundamental formulas, exploring different calculation methods, and being aware of potential pitfalls, you can confidently tackle percentage-related problems. This article provided a detailed exploration of calculating "7 out of 40 as a percentage," but the principles discussed extend far beyond this specific example. Mastering these techniques will significantly enhance your analytical abilities and problem-solving skills. Remember to practice regularly to solidify your understanding and build confidence in your calculations.
Latest Posts
Latest Posts
-
How Many Km Is 6000 Miles
May 11, 2025
-
What Is 10 Of 1 Cup
May 11, 2025
-
Como Hallar Un Lado De Un Triangulo
May 11, 2025
-
Pixels Per Inch To Dpi Converter
May 11, 2025
-
1 6 Hours Is How Many Minutes
May 11, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.