Common Factors Of 60 And 70
Treneri
May 13, 2025 · 5 min read
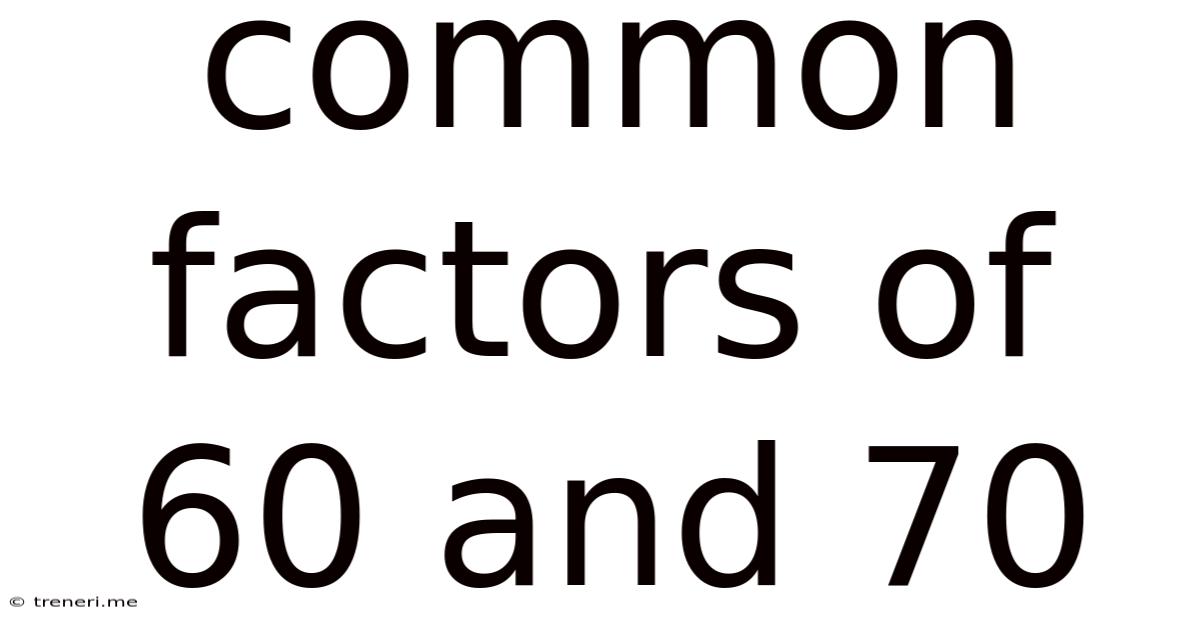
Table of Contents
Unveiling the Secrets: Finding the Common Factors of 60 and 70
Finding the common factors of two numbers might seem like a simple mathematical task, but understanding the underlying principles and exploring different approaches can illuminate fundamental concepts in number theory. This in-depth exploration delves into the common factors of 60 and 70, demonstrating various methods, and highlighting the significance of prime factorization in this process.
Understanding Factors and Common Factors
Before diving into the specifics of 60 and 70, let's solidify our understanding of key terminology:
-
Factor: A factor of a number is any integer that divides the number evenly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
-
Common Factor: A common factor of two or more numbers is a factor that is shared by all of them. For instance, the common factors of 12 and 18 are 1, 2, 3, and 6.
-
Greatest Common Factor (GCF): Also known as the highest common factor (HCF), this is the largest common factor among a set of numbers. The GCF of 12 and 18 is 6.
Method 1: Listing Factors
The most straightforward method for finding the common factors of 60 and 70 involves listing all factors of each number and then identifying the ones they have in common.
Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Factors of 70: 1, 2, 5, 7, 10, 14, 35, 70
Common Factors of 60 and 70: By comparing the two lists, we see that the common factors are 1, 2, 5, and 10.
This method is effective for smaller numbers, but it can become cumbersome and prone to errors as the numbers get larger.
Method 2: Prime Factorization
A more efficient and systematic approach utilizes prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
Let's find the prime factorization of 60 and 70:
-
60: 2 x 2 x 3 x 5 = 2² x 3 x 5
-
70: 2 x 5 x 7
Now, to find the common factors, we identify the prime factors that appear in both factorizations. In this case, we have 2 and 5.
To find all common factors, we consider all possible combinations of these common prime factors:
- 1: (No common prime factors)
- 2: (The prime factor 2)
- 5: (The prime factor 5)
- 10: (2 x 5)
Therefore, the common factors of 60 and 70 are 1, 2, 5, and 10. This method is far more efficient than listing all factors, especially for larger numbers.
Method 3: Greatest Common Factor (GCF) and its Relation to Common Factors
The greatest common factor (GCF) is the largest number that divides both 60 and 70 without leaving a remainder. Once we find the GCF, we can easily determine all common factors.
Using the prime factorization method:
-
Prime Factorization: We already established that 60 = 2² x 3 x 5 and 70 = 2 x 5 x 7.
-
Identify Common Prime Factors: Both factorizations contain 2 and 5.
-
Calculate GCF: The GCF is found by multiplying the common prime factors raised to the lowest power they appear in either factorization. In this case, the lowest power of 2 is 2¹ and the lowest power of 5 is 5¹. Therefore, the GCF(60, 70) = 2 x 5 = 10.
-
Finding all Common Factors: All common factors of 60 and 70 are the factors of the GCF (10). The factors of 10 are 1, 2, 5, and 10. Thus, the common factors are 1, 2, 5, and 10.
This approach is particularly useful when dealing with larger numbers where listing all factors becomes impractical. Finding the GCF first streamlines the process of identifying all common factors.
Exploring the Significance of Common Factors
Understanding common factors is crucial in various mathematical contexts:
-
Simplifying Fractions: Finding the GCF is essential for simplifying fractions to their lowest terms. For example, the fraction 60/70 can be simplified by dividing both the numerator and denominator by their GCF (10), resulting in the simplified fraction 6/7.
-
Solving Equations: In algebra, finding common factors helps simplify and solve equations.
-
Geometry: Common factors are used in geometry problems involving finding dimensions of shapes or determining the greatest common divisor of lengths.
-
Number Theory: The concept of common factors and the GCF forms the foundation for many advanced concepts in number theory, such as modular arithmetic and cryptography.
Beyond the Basics: Extending the Concept
The principles discussed here extend to finding common factors of more than two numbers. The process remains the same: find the prime factorization of each number, identify the common prime factors, and then generate all possible combinations of these factors. The GCF can also be easily extended to multiple numbers by using similar procedures.
Conclusion: Mastering the Art of Finding Common Factors
Finding the common factors of 60 and 70, as demonstrated, is a fundamental yet powerful concept in mathematics. While the simple listing method works for smaller numbers, prime factorization provides a more efficient and scalable approach, especially for larger numbers. Understanding the relationship between common factors and the GCF streamlines the process even further. Mastering these techniques provides a solid foundation for more advanced mathematical explorations and problem-solving. The ability to easily find common factors is a valuable skill with applications in numerous fields, emphasizing its importance in both theoretical and practical contexts. Remember, consistent practice and understanding the underlying principles are key to mastering this vital mathematical concept.
Latest Posts
Latest Posts
-
What Is A 60 As A Grade
May 13, 2025
-
Cuanto Es 100 Gramos En Cups
May 13, 2025
-
How Long Is 44 Days In Months
May 13, 2025
-
A Wave Of Frequency Of 1000 Hertz Vibrates At
May 13, 2025
-
8 Out Of 21 As A Percentage
May 13, 2025
Related Post
Thank you for visiting our website which covers about Common Factors Of 60 And 70 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.