Find The Perimeter Of The Quadrilateral In Simplest Form
Treneri
Apr 05, 2025 · 6 min read
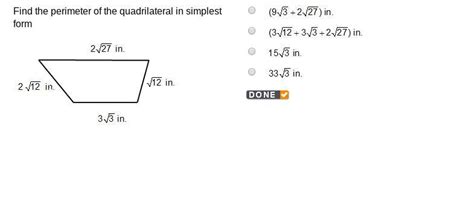
Table of Contents
Finding the Perimeter of a Quadrilateral: A Comprehensive Guide
Finding the perimeter of a quadrilateral might seem like a straightforward task, but understanding the nuances and different approaches involved can significantly improve your problem-solving skills in geometry. This comprehensive guide delves into various methods for calculating the perimeter, tackling different types of quadrilaterals and incorporating real-world applications to solidify your understanding.
Understanding Quadrilaterals and Perimeter
A quadrilateral is a polygon with four sides and four angles. The perimeter of any polygon, including a quadrilateral, is simply the total distance around its outer edges. In other words, it's the sum of the lengths of all its sides. This fundamental concept applies to all quadrilaterals, regardless of their shape or specific properties.
Formula for Perimeter:
The general formula for the perimeter (P) of any quadrilateral with side lengths a, b, c, and d is:
P = a + b + c + d
This formula remains consistent across all quadrilateral types, making it a versatile tool for various geometric problems.
Calculating Perimeter for Different Quadrilaterals
While the basic formula remains the same, the approach to finding the perimeter can vary slightly depending on the specific type of quadrilateral:
1. Square
A square is a quadrilateral with four equal sides and four right angles. If the length of one side is 's', then the perimeter is:
P = 4s
This simplified formula is extremely efficient for calculating the perimeter of a square. For example, if a square has a side length of 5 cm, the perimeter is 4 * 5 cm = 20 cm.
2. Rectangle
A rectangle is a quadrilateral with four right angles, with opposite sides being equal in length. Let's denote the length as 'l' and the width as 'w'. The perimeter is:
P = 2l + 2w or P = 2(l + w)
This formula is equally straightforward. A rectangle with a length of 8 meters and a width of 3 meters has a perimeter of 2(8m + 3m) = 22 meters.
3. Parallelogram
A parallelogram has opposite sides that are parallel and equal in length. Let's represent the lengths of the two sides as 'a' and 'b'. The perimeter is:
P = 2a + 2b
This is similar to the rectangle formula, highlighting the relationship between rectangles (a special case of a parallelogram) and parallelograms.
4. Rhombus
A rhombus is a quadrilateral with all four sides equal in length. If the side length is 's', then the perimeter is:
P = 4s
This formula is identical to the square's perimeter formula, emphasizing the relationship between rhombuses and squares (a special case of a rhombus).
5. Trapezoid (Trapezium)
A trapezoid (or trapezium) is a quadrilateral with at least one pair of parallel sides. There's no single simplified formula for the perimeter of a trapezoid, as the side lengths can be completely independent. Therefore, the general formula applies:
P = a + b + c + d
where a, b, c, and d are the lengths of the four sides.
6. Irregular Quadrilateral
An irregular quadrilateral is a quadrilateral with no specific properties; its sides and angles are all different. Again, the general formula is necessary:
P = a + b + c + d
It's crucial to accurately measure or be given the lengths of all four sides to determine the perimeter.
Solving Perimeter Problems: Step-by-Step Approach
Let's illustrate the process of finding the perimeter with a few examples:
Example 1: Finding the perimeter of a rectangle.
A rectangular garden measures 12 feet in length and 7 feet in width. Find the perimeter.
- Identify the type of quadrilateral: It's a rectangle.
- Recall the appropriate formula: P = 2(l + w)
- Substitute the given values: P = 2(12 feet + 7 feet)
- Calculate the perimeter: P = 2(19 feet) = 38 feet
Example 2: Finding the perimeter of an irregular quadrilateral.
An irregular quadrilateral has sides with lengths 5 cm, 8 cm, 11 cm, and 6 cm. Find the perimeter.
- Identify the type of quadrilateral: It's an irregular quadrilateral.
- Recall the appropriate formula: P = a + b + c + d
- Substitute the given values: P = 5 cm + 8 cm + 11 cm + 6 cm
- Calculate the perimeter: P = 30 cm
Example 3: A more complex problem involving a combination of shapes.
Imagine a figure composed of a square with side length 4m attached to a rectangle with length 6m and width 4m. Find the total perimeter of the combined shape.
- Break down the figure: The figure consists of a square and a rectangle.
- Calculate the perimeter of the square: P_square = 4 * 4m = 16m
- Calculate the perimeter of the rectangle: P_rectangle = 2(6m + 4m) = 20m
- Account for overlapping sides: The square and rectangle share a 4m side, so this length is counted twice in the individual perimeters. We need to subtract this overlapping length once (4m) from the total.
- Calculate the total perimeter: P_total = P_square + P_rectangle - 4m = 16m + 20m - 4m = 32m
Real-World Applications of Quadrilateral Perimeter
Understanding how to calculate the perimeter of quadrilaterals is essential in various real-world scenarios:
- Construction and Architecture: Calculating the amount of materials needed for fencing, building walls, or laying flooring often involves determining the perimeter of rectangular or irregular areas.
- Landscaping and Gardening: Determining the length of fencing required for a garden or the amount of edging for a walkway necessitates calculating the perimeter.
- Framing Pictures and Artwork: The amount of frame material needed is directly related to the perimeter of the picture.
- Sports Fields: The perimeter of a sports field is important for various purposes, including calculating the length of running tracks.
- Sewing and Fabric Cutting: Calculating the perimeter is critical for determining the amount of fabric needed for various projects.
Advanced Concepts and Challenges
While the basic principles of finding the perimeter are straightforward, advanced problems might involve:
- Finding missing side lengths: You might be given the perimeter and some side lengths, requiring you to solve for the unknown side(s). This involves algebraic manipulation of the perimeter formula.
- Problems involving composite figures: These problems often involve combining multiple quadrilaterals or other shapes, requiring careful analysis of overlapping sides.
- Problems involving angles and properties of specific quadrilaterals: Knowing the properties of different quadrilaterals (e.g., opposite sides are equal in a parallelogram) can significantly simplify the problem-solving process.
- Coordinate Geometry: Problems might involve finding the perimeter of a quadrilateral whose vertices are given as coordinates in a Cartesian plane. This requires using the distance formula to calculate the lengths of the sides.
Conclusion
Calculating the perimeter of a quadrilateral is a fundamental skill in geometry with wide-ranging applications. Mastering different approaches for various quadrilateral types and tackling increasingly complex problems will build a solid foundation in geometric problem-solving. Remember to always carefully identify the type of quadrilateral, apply the appropriate formula, and meticulously account for all sides to arrive at the accurate perimeter in its simplest form. By practicing regularly and applying your knowledge to real-world situations, you'll develop a strong intuitive understanding of this essential geometric concept.
Latest Posts
Latest Posts
-
Raw To Cooked Weight Conversion Calculator
Apr 05, 2025
-
Btu In Ton Of Air Conditioning
Apr 05, 2025
-
How To Find Length And Width From Perimeter
Apr 05, 2025
-
How Long Is 2000 Hours In Days
Apr 05, 2025
-
Cuanto Es Un Acre En Metros Cuadrados
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Find The Perimeter Of The Quadrilateral In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
