Find What Percent Of 5 Is 2
Treneri
May 10, 2025 · 4 min read
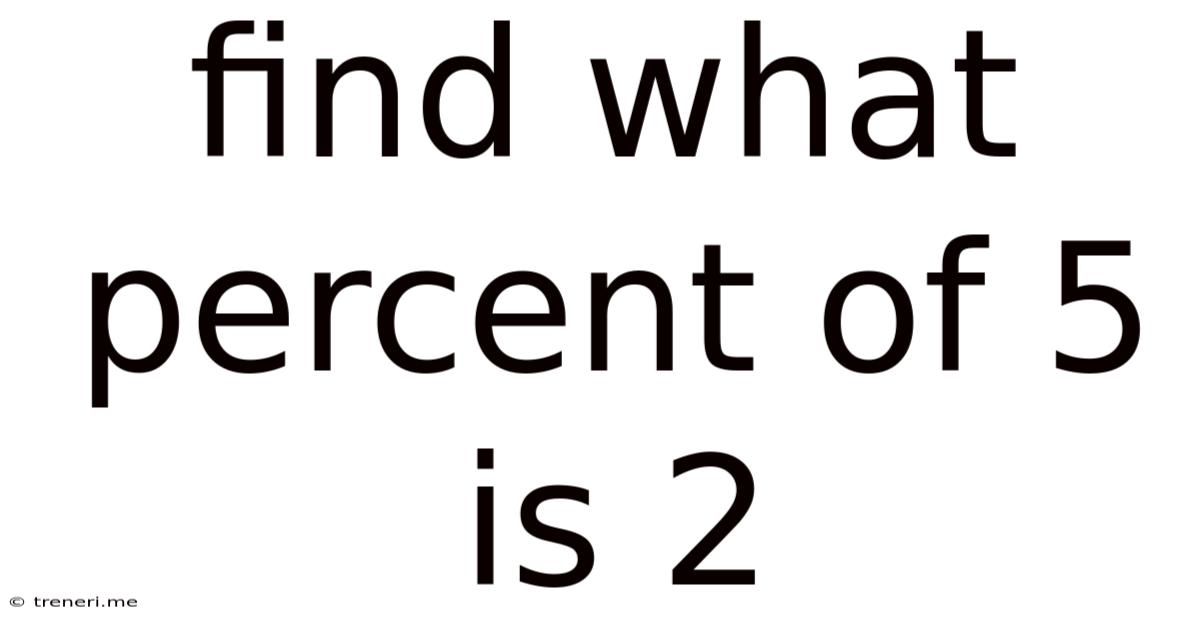
Table of Contents
Finding What Percent of 5 is 2: A Comprehensive Guide
Determining what percentage a number represents of another is a fundamental skill in mathematics with wide-ranging applications in various fields. This comprehensive guide delves into the process of calculating what percent of 5 is 2, providing multiple approaches, detailed explanations, and real-world examples. We will explore different methods, including using proportions, decimal conversion, and the percentage formula, ensuring a thorough understanding of the concept. We'll also touch upon related concepts and explore how to apply this knowledge to solve more complex percentage problems.
Understanding the Problem: What Percent of 5 is 2?
The core question, "What percent of 5 is 2?", asks us to find the percentage that 2 represents when considered as a part of the whole, which is 5. This can be visualized as a fraction: 2/5. Our goal is to express this fraction as a percentage. Remember that a percentage is simply a fraction expressed out of 100.
Method 1: Using Proportions
Proportions are a powerful tool for solving percentage problems. We can set up a proportion to solve this problem:
2/5 = x/100
Where:
- 2 represents the part.
- 5 represents the whole.
- x represents the unknown percentage we need to find.
- 100 represents the total percentage (100%).
To solve for x, we cross-multiply:
5x = 200
Now, divide both sides by 5:
x = 40
Therefore, 2 is 40% of 5.
Method 2: Decimal Conversion
This method involves converting the fraction into a decimal and then multiplying by 100 to express it as a percentage.
First, convert the fraction 2/5 into a decimal:
2 ÷ 5 = 0.4
Next, multiply the decimal by 100 to find the percentage:
0.4 x 100 = 40
Again, we find that 2 is 40% of 5.
Method 3: Using the Percentage Formula
The standard percentage formula is:
(Part / Whole) x 100 = Percentage
In our problem:
- Part = 2
- Whole = 5
Substituting these values into the formula:
(2 / 5) x 100 = Percentage
(0.4) x 100 = 40
Therefore, the percentage is 40%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples:
1. Discounts and Sales:
Imagine a shirt originally priced at $5 is on sale for $2. Using the methods discussed, we've already established that the discount is 40%. This knowledge is essential for consumers to understand the savings involved.
2. Grade Calculations:
If a student answers 2 out of 5 questions correctly on a quiz, their score is 40%. This method is widely used in education to calculate grades and assess student performance.
3. Financial Calculations:
Percentage calculations are fundamental in finance. For instance, calculating interest rates, investment returns, and tax rates all rely heavily on understanding percentages. If you invest $5 and receive a return of $2, your return is 40%.
4. Data Analysis:
Percentage calculations are extensively used in data analysis to represent proportions and trends within datasets. For example, if a survey shows that 2 out of 5 respondents prefer a particular product, this translates to a 40% preference rate.
Solving More Complex Percentage Problems
The principles used to determine what percent of 5 is 2 can be extended to solve more intricate percentage problems. Let's explore a few examples:
Example 1: Finding the Whole when the Percentage and Part are Known:
Suppose you know that 40% of a number is 8. How do you find the original number?
We can use the formula: (Part / Percentage) x 100 = Whole
In this case:
(8 / 40) x 100 = 20
The whole number is 20.
Example 2: Finding the Part when the Percentage and Whole are Known:
If 25% of a number is 10, how do you find the part (the 25%)?
The formula can be rearranged: (Percentage/100) x Whole = Part
In this case:
(25/100) x 40 = 10
The part (representing 25%) is 10.
Example 3: Percentage Increase or Decrease:
Let’s say a price increases from $5 to $7. To calculate the percentage increase:
- Find the difference: $7 - $5 = $2
- Divide the difference by the original price: $2 / $5 = 0.4
- Multiply by 100 to get the percentage increase: 0.4 x 100 = 40%
The price has increased by 40%. A similar approach can be used to calculate percentage decrease.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages is a versatile skill that extends far beyond basic arithmetic. By understanding the different methods – proportions, decimal conversion, and the percentage formula – you can confidently tackle various percentage-related problems in various contexts, including everyday life, academics, and professional settings. Practice applying these methods to a variety of examples to build a strong understanding and proficiency in this fundamental mathematical concept. Mastering these calculations will empower you to analyze data, interpret information, and make informed decisions in numerous situations. Remember that consistent practice is key to solidifying your understanding and building confidence in solving percentage problems of any complexity.
Latest Posts
Latest Posts
-
Lcm Of 2 4 And 5
May 11, 2025
-
26 Miles Equals How Many Kilometers
May 11, 2025
-
What Percentage Of People Can Dunk
May 11, 2025
-
What Is The Height Of The Prism
May 11, 2025
-
Greatest Common Factor Of 12 And 15
May 11, 2025
Related Post
Thank you for visiting our website which covers about Find What Percent Of 5 Is 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.