Gcf Of 35 56 And 63
Treneri
May 13, 2025 · 5 min read
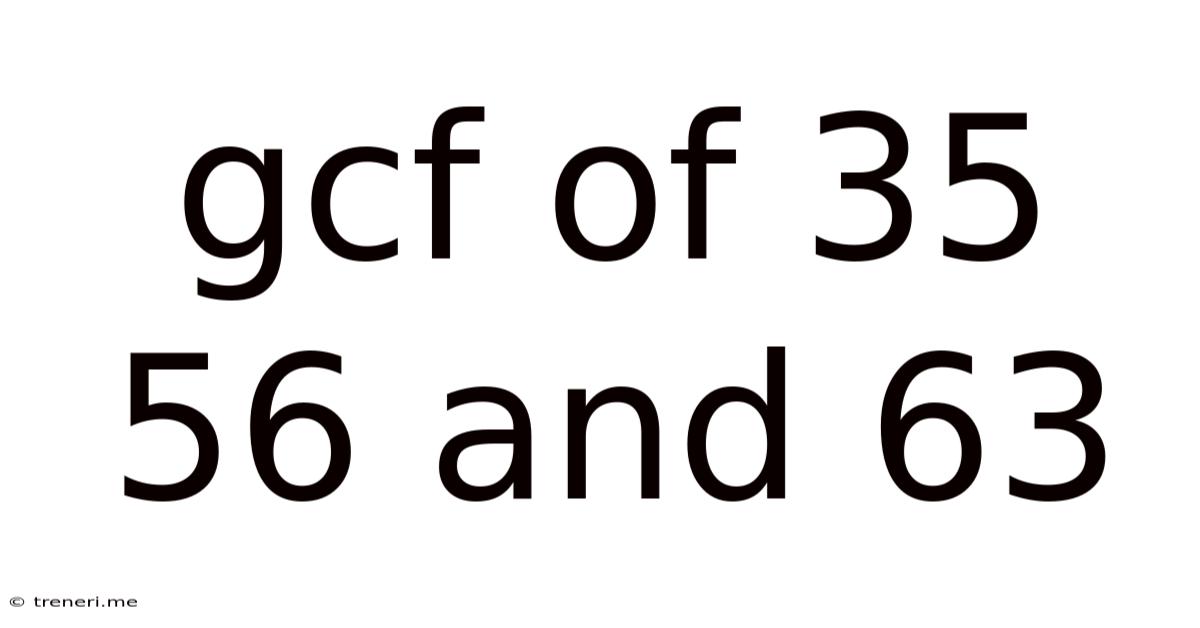
Table of Contents
Finding the Greatest Common Factor (GCF) of 35, 56, and 63: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of a set of numbers is a fundamental concept in mathematics with applications across various fields, from simplifying fractions to solving complex algebraic equations. This article will delve into the process of determining the GCF of 35, 56, and 63, exploring multiple methods and providing a comprehensive understanding of the underlying principles. We'll also touch upon the broader applications and significance of GCF in mathematics and beyond.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into all the given numbers evenly. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Methods for Finding the GCF of 35, 56, and 63
There are several efficient methods to calculate the GCF of a set of numbers. Let's explore the most common approaches:
1. Prime Factorization Method
This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Then, we identify the common prime factors and multiply them together to find the GCF.
- Prime factorization of 35: 5 x 7
- Prime factorization of 56: 2 x 2 x 2 x 7 = 2³ x 7
- Prime factorization of 63: 3 x 3 x 7 = 3² x 7
Examining the prime factorizations, we see that the only common prime factor among 35, 56, and 63 is 7. Therefore, the GCF of 35, 56, and 63 is 7.
2. Listing Factors Method
This method involves listing all the factors (divisors) of each number and then identifying the largest factor common to all.
- Factors of 35: 1, 5, 7, 35
- Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56
- Factors of 63: 1, 3, 7, 9, 21, 63
Comparing the lists, we find that the largest factor common to all three numbers is 7.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF. To extend this to three or more numbers, we find the GCF of the first two numbers and then find the GCF of that result and the third number, and so on.
Let's apply the Euclidean algorithm to 35, 56, and 63:
-
Find the GCF of 35 and 56:
- 56 = 1 x 35 + 21
- 35 = 1 x 21 + 14
- 21 = 1 x 14 + 7
- 14 = 2 x 7 + 0 The GCF of 35 and 56 is 7.
-
Find the GCF of 7 and 63:
- 63 = 9 x 7 + 0 The GCF of 7 and 63 is 7.
Therefore, the GCF of 35, 56, and 63 is 7.
Applications of the Greatest Common Factor
The concept of GCF extends far beyond simple mathematical exercises. It has numerous practical applications in various fields:
1. Simplifying Fractions
The GCF is crucial for simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF. For example, to simplify the fraction 21/49, we find the GCF of 21 and 49, which is 7. Dividing both the numerator and denominator by 7 gives us the simplified fraction 3/7.
2. Solving Algebraic Equations
GCF plays a significant role in factoring algebraic expressions. Factoring involves expressing an algebraic expression as a product of simpler expressions. Finding the GCF of the terms in an expression allows us to factor out the common factor, simplifying the expression and making it easier to solve.
3. Geometry and Measurement
GCF is used in geometric problems involving finding the dimensions of objects with specific properties. For example, finding the largest square tile that can perfectly cover a rectangular floor requires determining the GCF of the length and width of the floor.
4. Real-World Applications
Beyond theoretical mathematics, GCF finds applications in various practical scenarios:
- Resource allocation: Determining the most efficient way to divide resources among different groups often involves finding the GCF.
- Scheduling: Organizing schedules or events that need to align with multiple time intervals might require the use of GCF to find the common time slots.
- Manufacturing: In manufacturing processes, finding the GCF can help in optimizing production by determining the most efficient cutting or packaging sizes.
Expanding on the Concept: Least Common Multiple (LCM)
While this article focuses on GCF, it's important to mention the closely related concept of the Least Common Multiple (LCM). The LCM of two or more integers is the smallest positive integer that is a multiple of all the integers. GCF and LCM are interconnected; their product is equal to the product of the original numbers. This relationship is expressed as:
GCF(a, b) x LCM(a, b) = a x b
This relationship can be extended to more than two numbers as well. Understanding both GCF and LCM provides a comprehensive understanding of number theory and its practical applications.
Conclusion: Mastering GCF Calculations
Mastering the calculation of the greatest common factor is an essential skill in mathematics. Understanding the various methods – prime factorization, listing factors, and the Euclidean algorithm – equips you with the tools to solve problems efficiently, regardless of the size of the numbers involved. The applications of GCF extend far beyond textbook exercises, impacting various fields and offering practical solutions to real-world problems. By understanding this fundamental concept, you build a strong foundation for more advanced mathematical concepts and problem-solving skills. Remember to practice regularly to solidify your understanding and improve your speed and accuracy in calculating GCF. The ability to quickly and accurately determine the GCF will prove invaluable in many mathematical and real-world applications.
Latest Posts
Latest Posts
-
What Is The Factor Of 83
May 13, 2025
-
850 Ml Is How Many Ounces
May 13, 2025
-
1 2 Divided By 5 8 As A Fraction
May 13, 2025
-
What Uv Index Can You Tan At
May 13, 2025
-
What Is The Perimeter Of The Parallelogram Shown Below
May 13, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 35 56 And 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.