How To Find Side Length Of Octagon
Treneri
Apr 05, 2025 · 5 min read
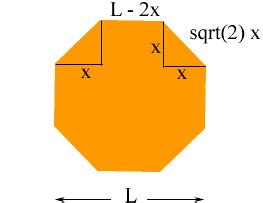
Table of Contents
How to Find the Side Length of an Octagon: A Comprehensive Guide
Finding the side length of an octagon can seem daunting, but with the right approach and understanding of different octagon types, it becomes manageable. This comprehensive guide breaks down various methods, catering to different levels of mathematical understanding and the specific information available. We'll explore calculating side lengths for regular octagons (all sides and angles equal) and irregular octagons (sides and angles vary).
Understanding Octagons: Regular vs. Irregular
Before diving into calculations, it's crucial to distinguish between regular and irregular octagons. This distinction significantly impacts the approach you'll need to take.
Regular Octagon: A regular octagon possesses eight equal sides and eight equal angles (each measuring 135°). This symmetry allows for simpler calculations.
Irregular Octagon: An irregular octagon has sides and angles of varying lengths and measures. Determining the side length of an irregular octagon requires more information and often involves more complex methods, such as trigonometry or vector analysis. We might need additional information, like coordinates of vertices or lengths of diagonals.
Calculating Side Lengths of Regular Octagons
Several methods can determine the side length of a regular octagon, depending on the given information:
Method 1: Using the Circumradius (R)
The circumradius is the distance from the center of the octagon to each of its vertices. If you know the circumradius (R), the side length (s) can be calculated using the following formula:
s = 2R * sin(π/8)
or equivalently:
s = 2R * sin(22.5°)
This formula leverages the trigonometric properties of a regular octagon. Remember that π (pi) represents approximately 3.14159. You'll need a calculator with trigonometric functions to compute the sine of 22.5°.
Example: If the circumradius of a regular octagon is 10 cm, the side length is:
s = 2 * 10 cm * sin(22.5°) ≈ 7.65 cm
Method 2: Using the Apothem (a)
The apothem (a) is the distance from the center of the octagon to the midpoint of any side. This method involves a slightly different trigonometric approach:
s = 2a * tan(π/8)
or equivalently:
s = 2a * tan(22.5°)
Example: If the apothem of a regular octagon is 8 cm, the side length is:
s = 2 * 8 cm * tan(22.5°) ≈ 6.9 cm
Method 3: Using the Area (A)
The area of a regular octagon can also be used to determine its side length. The formula for the area of a regular octagon is:
A = 2(1 + √2) * s²
To find the side length (s), rearrange the formula:
s = √[A / (2(1 + √2))]
Example: If the area of a regular octagon is 100 cm², the side length is:
s = √[100 cm² / (2(1 + √2))] ≈ 4.2 cm
Calculating Side Lengths of Irregular Octagons
Determining the side length of an irregular octagon is significantly more complex and often requires additional information. There's no single universal formula. The approach depends heavily on what data is provided.
Method 1: Using Coordinates
If you have the coordinates of all eight vertices of the irregular octagon, you can use the distance formula to calculate the length of each side. The distance formula between two points (x₁, y₁) and (x₂, y₂) is:
distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Apply this formula to each pair of consecutive vertices to find the lengths of all eight sides.
Method 2: Using Trigonometry and Known Information
You might have some combination of side lengths, angles, or diagonal lengths. In these scenarios, you'll likely need to use trigonometric functions (sine, cosine, tangent) within a series of triangles formed within the octagon. This often involves breaking down the octagon into smaller, solvable triangles and using the Law of Sines or the Law of Cosines. This is very situation-specific, and a visual representation (diagram) of the octagon with known dimensions is crucial.
Example Scenario: Imagine you know three consecutive side lengths (a, b, c) and the angles between them. You could use the Law of Cosines to find the length of a diagonal, and then continue applying trigonometric principles to determine other side lengths. However, the exact steps heavily depend on the available data.
Method 3: Advanced Techniques (Vector Analysis)
For highly complex irregular octagons, vector analysis provides a powerful but advanced method. Representing sides as vectors and applying vector addition, subtraction, and dot product calculations allows for precise side length determination. This technique is significantly more intricate and requires a strong understanding of vector mathematics.
Practical Applications
Understanding how to calculate octagon side lengths has practical applications in various fields:
-
Architecture and Construction: Designing octagonal buildings or structures requires accurate calculations of side lengths for materials and measurements.
-
Engineering: Octagonal shapes appear in engineering designs, such as gears, components, and structural elements. Accurate side length determination is crucial for functionality.
-
Graphic Design and Computer-Aided Design (CAD): Creating precise octagonal designs in digital environments demands the ability to calculate side lengths based on the desired dimensions and specifications.
Conclusion
Finding the side length of an octagon involves different approaches depending on whether it's regular or irregular and the information available. For regular octagons, simple formulas using circumradius, apothem, or area are sufficient. Irregular octagons require more advanced techniques, such as coordinate geometry, trigonometry, or vector analysis. Understanding these methods allows for precise calculations in various applications, from construction to design. Remember, visualization and accurate measurements are key to success in these calculations. Always double-check your work and use appropriate tools for accuracy.
Latest Posts
Latest Posts
-
How Many Calories Burned On Elliptical Trainer
Apr 06, 2025
-
How To Find A Slope Of A Triangle
Apr 06, 2025
-
Florida Tax Tag And Title Calculator
Apr 06, 2025
-
90 Days From July 17 2024
Apr 06, 2025
-
Least Common Denominator Of 8 And 4
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How To Find Side Length Of Octagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
