Is 2 1/3 Equal To 2/3
Treneri
May 12, 2025 · 5 min read
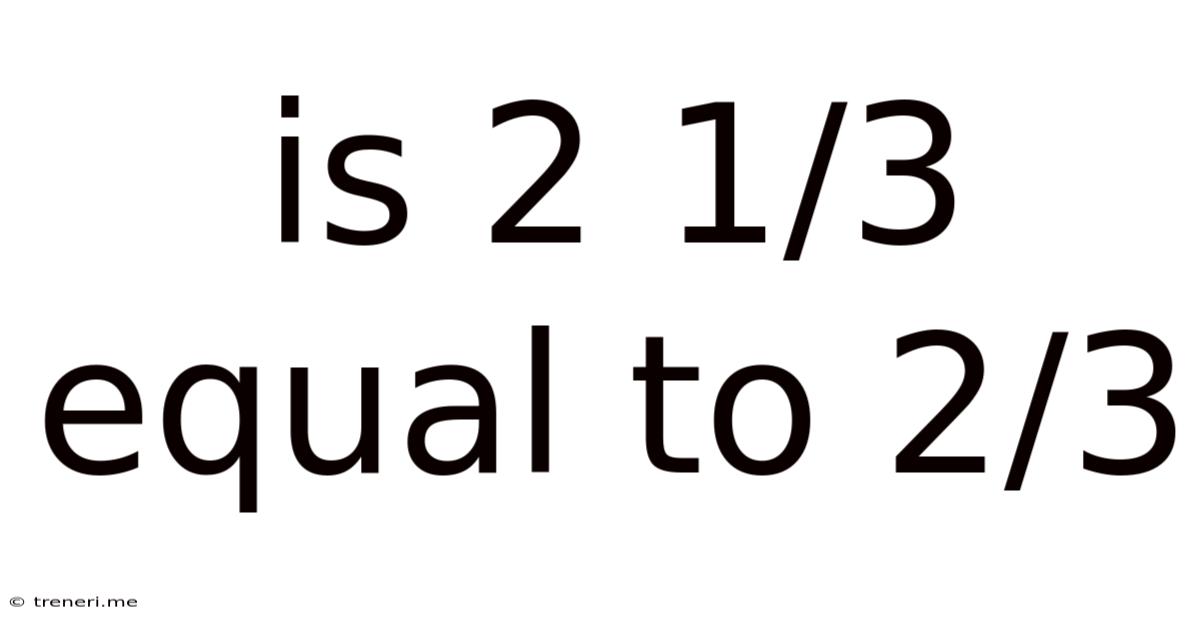
Table of Contents
Is 2 1/3 Equal to 2/3? A Deep Dive into Fraction Comparison
The question, "Is 2 1/3 equal to 2/3?" is a seemingly simple one, yet it highlights a fundamental misunderstanding about fractions that many struggle with. The short answer is a resounding no, but understanding why requires a deeper exploration of fraction representation, comparison, and the importance of proper mathematical manipulation. This article will dissect the problem, providing clear explanations and examples to solidify your understanding of fractions and mixed numbers.
Understanding Fractions and Mixed Numbers
Before we dive into the comparison, let's define our terms:
Fraction: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, 1/2 represents one out of two equal parts.
Mixed Number: A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). For example, 2 1/3 represents two whole units plus one-third of another unit.
Improper Fraction: An improper fraction is where the numerator is greater than or equal to the denominator. For example, 7/3 is an improper fraction. Improper fractions can be converted to mixed numbers and vice-versa.
Converting Mixed Numbers to Improper Fractions
To effectively compare fractions, especially when one is a mixed number, it's crucial to convert them to a common format – usually improper fractions. Here's how to convert a mixed number to an improper fraction:
-
Multiply the whole number by the denominator: In our example, 2 1/3, we multiply 2 (the whole number) by 3 (the denominator). This gives us 6.
-
Add the numerator: Add the result from step 1 to the numerator of the fraction. 6 + 1 = 7.
-
Keep the same denominator: The denominator remains unchanged. In this case, it's 3.
Therefore, 2 1/3 is equal to the improper fraction 7/3.
Comparing Fractions: A Visual Approach
Let's visualize the difference between 2 1/3 and 2/3. Imagine a pizza cut into three equal slices.
-
2/3: This represents two out of three slices. You have two-thirds of the pizza.
-
2 1/3: This represents two whole pizzas plus one-third of another pizza. You have significantly more pizza than with 2/3.
This visual representation clearly shows that 2 1/3 is much larger than 2/3.
Comparing Fractions: A Numerical Approach
The numerical approach involves finding a common denominator if the denominators are different. In this case, we've already converted 2 1/3 to the improper fraction 7/3. Now we can directly compare:
- 7/3 and 2/3
Since the denominators are the same, we simply compare the numerators: 7 is much greater than 2. Therefore, 7/3 > 2/3, confirming that 2 1/3 is not equal to 2/3.
Common Mistakes to Avoid
Many errors arise from a misunderstanding of fraction representation and manipulation. Here are some common mistakes to watch out for:
-
Ignoring the whole number: A common mistake is to simply compare the numerators and ignore the whole number in a mixed number. This leads to incorrect conclusions. Always convert mixed numbers to improper fractions before comparison.
-
Incorrect conversion to improper fractions: Ensure you accurately follow the steps to convert mixed numbers to improper fractions. A simple error in the calculation will lead to an incorrect comparison.
-
Not finding a common denominator: When comparing fractions with different denominators, finding a common denominator is crucial. Comparing fractions directly without finding a common denominator often leads to inaccurate results.
Practical Applications: Real-World Examples
Understanding fraction comparison is essential in various real-world scenarios:
-
Cooking and Baking: Recipes often require precise measurements using fractions. Incorrect fraction comparison can lead to improperly proportioned ingredients and a failed recipe.
-
Construction and Engineering: Accurate calculations involving fractions are vital in construction and engineering projects. Errors in fraction comparison can have serious consequences.
-
Finance and Accounting: Financial calculations often involve fractions, especially when dealing with percentages, interest rates, and stock prices.
-
Data Analysis: In data analysis, understanding and comparing fractions is essential for interpreting data and drawing accurate conclusions.
Further Exploration: More Complex Fraction Comparisons
The principles discussed in this article apply to more complex fraction comparisons as well. For example, consider comparing 3 2/5 and 17/5. By converting 3 2/5 to an improper fraction (17/5), we find that they are equal. This highlights the importance of consistent application of conversion methods.
Conclusion: Mastering Fraction Comparison
The question, "Is 2 1/3 equal to 2/3?" serves as an excellent starting point for understanding the importance of correctly manipulating and comparing fractions. By mastering the conversion of mixed numbers to improper fractions, and by understanding the importance of finding a common denominator when comparing fractions with different denominators, one can confidently tackle more complex fraction-related problems. Remember to always visualize, if possible, and meticulously follow the mathematical steps to avoid common errors. This knowledge will prove invaluable in various aspects of life, from everyday tasks to more complex academic and professional endeavors. The ability to confidently and accurately compare fractions is a cornerstone of numerical literacy.
Latest Posts
Latest Posts
-
Calculating Time Of Death Using Rigor Mortis
May 13, 2025
-
Area Of Inscribed Square In A Circle
May 13, 2025
-
What Is The Greatest Common Factor Of 9 And 4
May 13, 2025
-
How Many Miles Is A 2 5 K
May 13, 2025
-
What Grade Is 23 Out Of 30
May 13, 2025
Related Post
Thank you for visiting our website which covers about Is 2 1/3 Equal To 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.