Is 3 4 Equivalent To 6 8
Treneri
May 10, 2025 · 5 min read
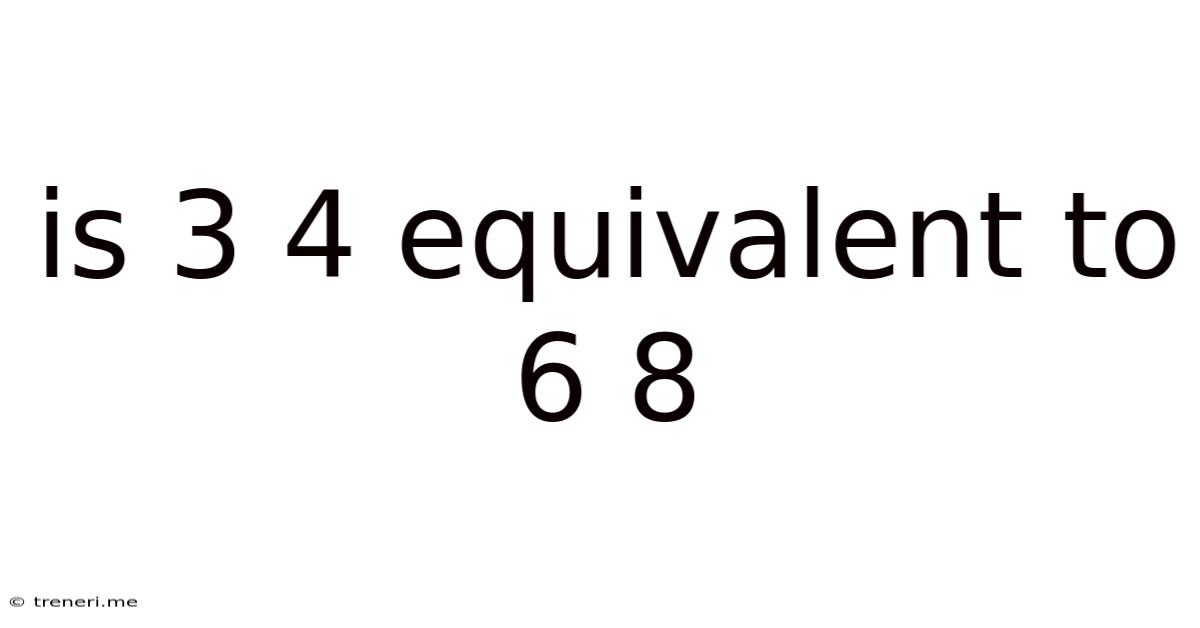
Table of Contents
Is 3/4 Equivalent to 6/8? A Deep Dive into Fraction Equivalence
The question, "Is 3/4 equivalent to 6/8?" might seem simple at first glance. For many, the answer is an immediate "yes," and intuitively, they're correct. However, a deeper understanding of fraction equivalence involves exploring the underlying mathematical concepts, demonstrating the equivalence through various methods, and understanding its implications in different mathematical contexts. This article aims to provide a comprehensive explanation suitable for students of various levels, from elementary school to those refreshing their foundational math skills.
Understanding Fractions: A Quick Refresher
Before diving into the equivalence of 3/4 and 6/8, let's quickly review the fundamental components of a fraction:
- Numerator: The top number in a fraction. It represents the number of parts you have. In 3/4, the numerator is 3.
- Denominator: The bottom number in a fraction. It represents the total number of equal parts the whole is divided into. In 3/4, the denominator is 4.
A fraction, therefore, represents a part of a whole. 3/4 means you have 3 out of 4 equal parts of a whole.
Methods to Prove Equivalence of 3/4 and 6/8
Several methods can be used to demonstrate that 3/4 and 6/8 represent the same value:
1. Simplifying Fractions: Finding the Simplest Form
Simplifying a fraction means reducing it to its lowest terms. We do this by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
- Finding the GCD of 6 and 8: The GCD of 6 and 8 is 2.
- Simplifying 6/8: Dividing both the numerator and denominator by 2, we get 6/2 = 3 and 8/2 = 4. This simplifies 6/8 to 3/4.
Since 6/8 simplifies to 3/4, it confirms their equivalence.
2. Multiplying the Numerator and Denominator: Creating Equivalent Fractions
We can create equivalent fractions by multiplying both the numerator and the denominator by the same non-zero number. This doesn't change the value of the fraction because it's essentially multiplying by 1 (e.g., 2/2 = 1).
- Multiplying 3/4: If we multiply both the numerator and denominator of 3/4 by 2, we get (3 x 2) / (4 x 2) = 6/8.
This method clearly shows that multiplying 3/4 by 1 (in the form of 2/2) results in 6/8, demonstrating their equivalence.
3. Visual Representation: Using Diagrams
Visual aids can effectively illustrate the equivalence. Imagine a pizza cut into four equal slices (representing the denominator 4). If you have 3 slices (numerator 3), you have 3/4 of the pizza.
Now, imagine the same pizza cut into eight equal slices (denominator 8). If you have 6 slices (numerator 6), you still have the same amount of pizza – 6/8. Both 3/4 and 6/8 represent the same portion of the whole pizza.
4. Decimal Representation: Converting to Decimals
Converting fractions to decimals provides another way to compare their values.
- Converting 3/4 to a decimal: 3 ÷ 4 = 0.75
- Converting 6/8 to a decimal: 6 ÷ 8 = 0.75
Since both fractions result in the same decimal value (0.75), they are equivalent.
Beyond the Basics: Implications of Fraction Equivalence
Understanding fraction equivalence is crucial for various mathematical operations and applications:
1. Addition and Subtraction of Fractions: Finding Common Denominators
Adding or subtracting fractions requires them to have a common denominator. Finding equivalent fractions with a common denominator is a fundamental step in this process. For example, adding 1/2 and 3/4 requires finding an equivalent fraction for 1/2 with a denominator of 4 (which is 2/4).
2. Comparing Fractions: Determining Greater or Lesser Values
Equivalence helps determine which of two fractions is larger or smaller. If you can express both fractions with a common denominator, comparing their numerators directly determines which fraction is greater.
3. Ratios and Proportions: Understanding Relationships
Fractions are directly related to ratios and proportions. Equivalent fractions represent equal ratios. For example, the ratio 3:4 is equivalent to the ratio 6:8. This concept is critical in fields like scaling, mixing ingredients, and many other real-world applications.
4. Algebra and Equation Solving: Manipulating Fractions
Fraction equivalence is essential in algebraic manipulations. We often simplify or transform fractions to solve equations and inequalities. For instance, when solving equations with fractions, we might need to find equivalent fractions to simplify the equation and isolate the variable.
5. Geometry and Measurement: Working with Units
Fractions are fundamental in geometry and measurement. Equivalence helps in converting units of measurement (e.g., inches to feet, centimeters to meters). For example, understanding that 1/2 is equivalent to 2/4 or 50/100 is crucial in various geometric calculations and measurement conversions.
Addressing Common Misconceptions
While the equivalence of 3/4 and 6/8 is straightforward, some misconceptions can arise:
- Confusing simplification with changing the value: Simplifying a fraction only changes its form, not its value. The simplified fraction represents the same portion of the whole as the original fraction.
- Incorrectly multiplying or dividing only the numerator or denominator: To create equivalent fractions, both the numerator and denominator must be multiplied or divided by the same non-zero number.
Conclusion: The Significance of Understanding Fraction Equivalence
The seemingly simple question of whether 3/4 is equivalent to 6/8 opens the door to a deeper exploration of fraction fundamentals. Understanding fraction equivalence isn't merely about memorizing a fact; it's about grasping the underlying mathematical principles that govern fraction representation and manipulation. This understanding is fundamental to success in higher-level mathematics, as well as crucial for various real-world applications involving ratios, proportions, measurement, and more. Mastering this concept builds a strong mathematical foundation, enabling greater fluency and comprehension in various mathematical domains. By utilizing different methods—simplification, multiplication, visual representations, and decimal conversions—we can confidently confirm that 3/4 and 6/8 are indeed equivalent representations of the same value.
Latest Posts
Latest Posts
-
What Fraction Is Equal To 6 8
May 10, 2025
-
101 Km To Miles Per Hour
May 10, 2025
-
What Is 25 Percent Of 4000
May 10, 2025
-
How Much Does 5 Cubic Feet Of Ice Weigh
May 10, 2025
-
Cuantos Dias Tiene El Mes De Abril
May 10, 2025
Related Post
Thank you for visiting our website which covers about Is 3 4 Equivalent To 6 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.