Lcm Of 3 10 And 5
Treneri
May 09, 2025 · 5 min read
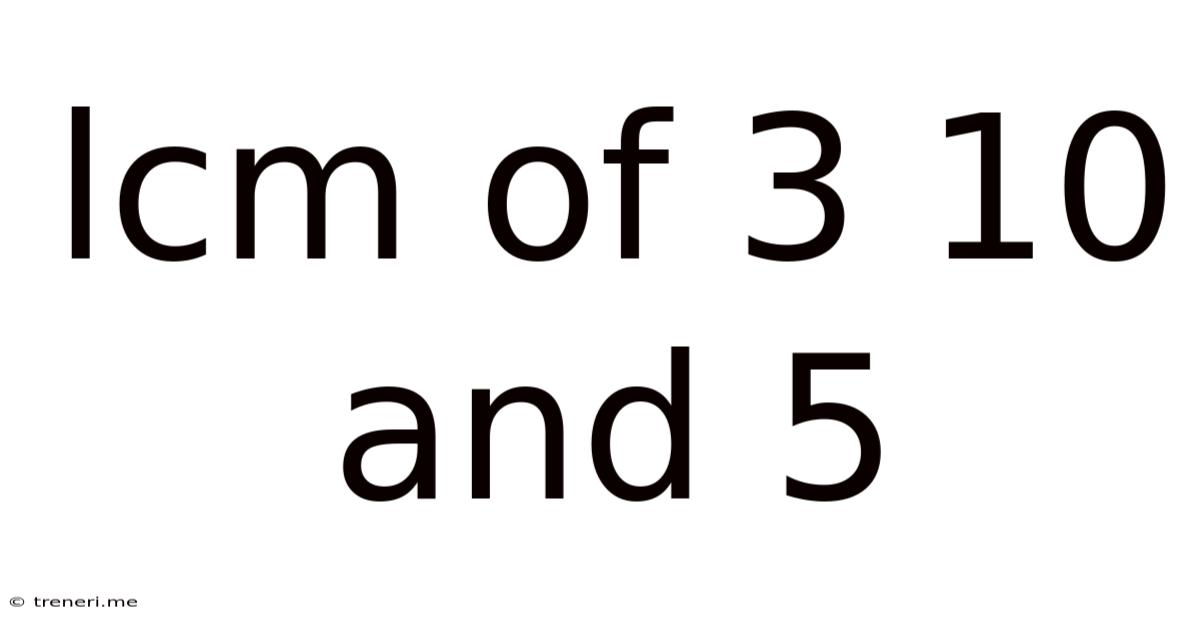
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 10, and 5: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to find the LCM is crucial for various applications, from simplifying fractions to solving problems in algebra and beyond. This article will provide a thorough explanation of how to calculate the LCM of 3, 10, and 5, exploring different methods and highlighting the underlying principles. We'll also delve into the broader context of LCMs and their significance.
Understanding Least Common Multiples
Before we tackle the specific problem of finding the LCM of 3, 10, and 5, let's establish a clear understanding of what an LCM is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12… and the multiples of 3 are 3, 6, 9, 12, 15… The common multiples of 2 and 3 are 6, 12, 18… The least common multiple is 6.
Method 1: Listing Multiples
The simplest method for finding the LCM of small numbers, like 3, 10, and 5, is to list the multiples of each number until you find a common multiple.
Step 1: List the multiples of each number:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30…
- Multiples of 10: 10, 20, 30, 40, 50…
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35…
Step 2: Identify the common multiples:
Looking at the lists above, we can see that 30 is a common multiple of 3, 10, and 5.
Step 3: Determine the least common multiple:
Since 30 is the smallest number that appears in all three lists, the LCM of 3, 10, and 5 is 30.
This method is straightforward for small numbers, but it becomes less efficient as the numbers get larger.
Method 2: Prime Factorization
A more efficient and systematic method for finding the LCM, especially for larger numbers, is the prime factorization method. This method involves breaking down each number into its prime factors.
Step 1: Find the prime factorization of each number:
- 3 = 3 (3 is a prime number)
- 10 = 2 × 5
- 5 = 5 (5 is a prime number)
Step 2: Identify the highest power of each prime factor:
Looking at the prime factorizations, we have the prime factors 2, 3, and 5. The highest power of each prime factor is:
- 2¹ = 2
- 3¹ = 3
- 5¹ = 5
Step 3: Multiply the highest powers together:
Multiply the highest powers of each prime factor to find the LCM:
LCM(3, 10, 5) = 2 × 3 × 5 = 30
This method is more efficient than listing multiples, particularly when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. There's a formula that connects the two:
LCM(a, b) × GCD(a, b) = a × b
This formula works for two numbers. For more than two numbers, you can apply it iteratively. First find the LCM of two numbers, then find the LCM of that result and the next number, and so on. However, for finding the GCD, we can use the Euclidean Algorithm which is very efficient.
Step 1: Find the GCD of 3 and 10 using the Euclidean Algorithm:
- Divide 10 by 3: 10 = 3 × 3 + 1
- The remainder is 1. Since the remainder is 1, the GCD(3,10) is 1.
Step 2: Find the GCD of the result (1) and 5:
Since GCD(1,5) = 1
Step 3: Use the formula to find the LCM:
While the formula directly doesn't apply to three numbers efficiently this way, it demonstrates the relationship between GCD and LCM. We already found the LCM using prime factorization to be 30.
Applications of LCM
The least common multiple has numerous applications across various mathematical fields and practical scenarios. Here are a few examples:
-
Adding and Subtracting Fractions: Finding the LCM of the denominators is essential when adding or subtracting fractions with different denominators. This allows you to rewrite the fractions with a common denominator, enabling the addition or subtraction operation.
-
Scheduling and Timing Problems: LCM is crucial in solving problems related to scheduling events that occur at regular intervals. For example, determining when two machines will complete their cycles simultaneously or when two trains will arrive at the same station again.
-
Modular Arithmetic: LCM plays a significant role in modular arithmetic, a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value—the modulus. This is applied in cryptography and computer science.
LCM of Larger Numbers
The methods described above, particularly prime factorization, are readily applicable to larger numbers. Let's consider finding the LCM of 12, 18, and 24:
Step 1: Prime Factorization:
- 12 = 2² × 3
- 18 = 2 × 3²
- 24 = 2³ × 3
Step 2: Highest Powers:
- 2³ = 8
- 3² = 9
Step 3: Multiply:
LCM(12, 18, 24) = 2³ × 3² = 8 × 9 = 72
Conclusion
Finding the least common multiple is a fundamental skill in mathematics with practical applications in various fields. While listing multiples works for small numbers, prime factorization provides a more efficient and generalizable method, especially for larger numbers. Understanding the relationship between LCM and GCD further enhances one's ability to solve problems involving these concepts. Mastering LCM calculations is essential for success in algebra, number theory, and various other mathematical disciplines. This comprehensive guide has equipped you with the knowledge and techniques to confidently tackle LCM problems of varying complexity.
Latest Posts
Latest Posts
-
How Many Cups Is 510 Grams
May 10, 2025
-
Solve The Inequality Write The Solution In Interval Notation
May 10, 2025
-
How Many Pounds Is 41 Kilos
May 10, 2025
-
24 Is What Percent Of 27
May 10, 2025
-
How Many Fluid Ounces Is 4 Cups
May 10, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 10 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.