Lcm Of 3 5 And 9
Treneri
May 11, 2025 · 5 min read
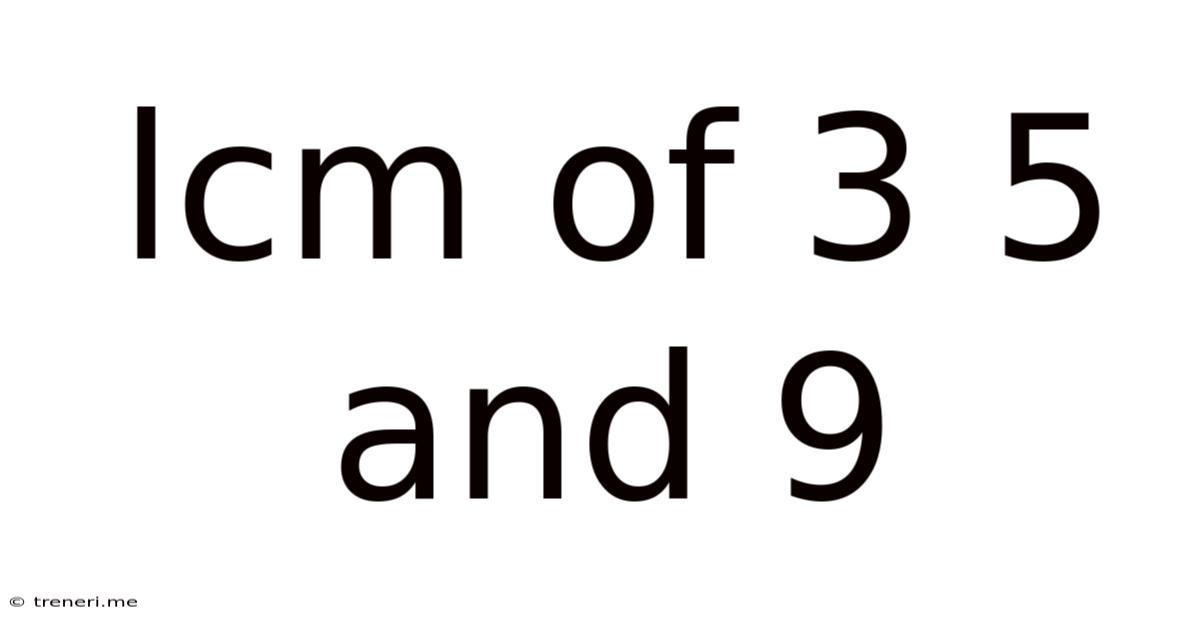
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 5, and 9: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to scheduling events. This comprehensive guide will delve into the process of determining the LCM of 3, 5, and 9, exploring various methods and providing a deeper understanding of the underlying principles. We'll also touch upon the broader context of LCMs and their importance in various mathematical fields.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 3, 5, and 9, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90...
By inspecting the lists, we can see that the smallest number common to all three lists is 45. Therefore, the LCM of 3, 5, and 9 is 45.
This method is simple to understand but can become cumbersome for larger numbers or a greater number of integers.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It involves breaking down each number into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself.
-
Prime Factorization:
- 3 = 3 (3 is a prime number)
- 5 = 5 (5 is a prime number)
- 9 = 3 x 3 = 3²
-
Identify the highest power of each prime factor:
- The prime factors involved are 3 and 5.
- The highest power of 3 is 3² = 9
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together:
- LCM(3, 5, 9) = 3² x 5 = 9 x 5 = 45
This method is more systematic and avoids the potentially lengthy process of listing multiples. It's particularly useful when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
While this formula is typically used for two numbers, we can extend the concept to three numbers by finding the LCM of the LCM of two numbers and the third number.
-
Find the GCD of any two numbers: Let's find the GCD of 3 and 5. Since 3 and 5 are both prime numbers and have no common factors other than 1, their GCD is 1.
-
Find the LCM of those two numbers using the formula: LCM(3, 5) x GCD(3, 5) = 3 x 5 LCM(3, 5) x 1 = 15 LCM(3, 5) = 15
-
Now find the LCM of the result and the remaining number: We need to find the LCM of 15 and 9.
-
Prime Factorization (for LCM(15,9)):
- 15 = 3 x 5
- 9 = 3 x 3 = 3²
-
Highest powers: 3² and 5
-
Multiply: 3² x 5 = 9 x 5 = 45
Therefore, the LCM(3, 5, 9) = 45. This method demonstrates the interconnectedness of LCM and GCD, offering another pathway to the solution.
Applications of LCM
The concept of LCM has diverse applications across various fields:
-
Fraction Arithmetic: Finding the LCM of the denominators is crucial for adding or subtracting fractions. This allows us to find a common denominator, simplifying the process.
-
Scheduling Problems: Imagine coordinating events that repeat at different intervals. The LCM helps determine when those events will occur simultaneously. For example, if one event happens every 3 days and another every 5 days, the LCM (15) tells us they'll coincide every 15 days.
-
Modular Arithmetic: LCM plays a significant role in modular arithmetic, a branch of number theory that deals with remainders after division.
-
Music Theory: The LCM is used in music theory to determine the least common denominator for rhythmic patterns.
-
Computer Science: LCM finds applications in computer algorithms and scheduling tasks within operating systems.
Conclusion
Finding the LCM of 3, 5, and 9, while seemingly a simple problem, offers a gateway to understanding broader mathematical concepts. We've explored three distinct methods—listing multiples, prime factorization, and using the GCD—each providing a unique perspective on this fundamental calculation. Understanding these methods is crucial for tackling more complex LCM problems and appreciating its importance across various disciplines. The LCM, a seemingly simple concept, reveals its profound significance as we delve into its various applications. Mastering the calculation and comprehension of the LCM contributes to a solid foundation in mathematics and problem-solving. Remember, the ability to efficiently and accurately calculate the LCM empowers you to tackle more advanced mathematical problems and enhances your problem-solving abilities across multiple fields.
Latest Posts
Latest Posts
-
4 5 As An Improper Fraction
May 13, 2025
-
1994 How Old Am I 2024
May 13, 2025
-
How Many Mm In 9 Cm
May 13, 2025
-
7 Out Of 21 As A Percentage
May 13, 2025
-
What Is The Greatest Common Factor Of 18 And 35
May 13, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 5 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.