Lcm Of 7 3 And 5
Treneri
May 12, 2025 · 5 min read
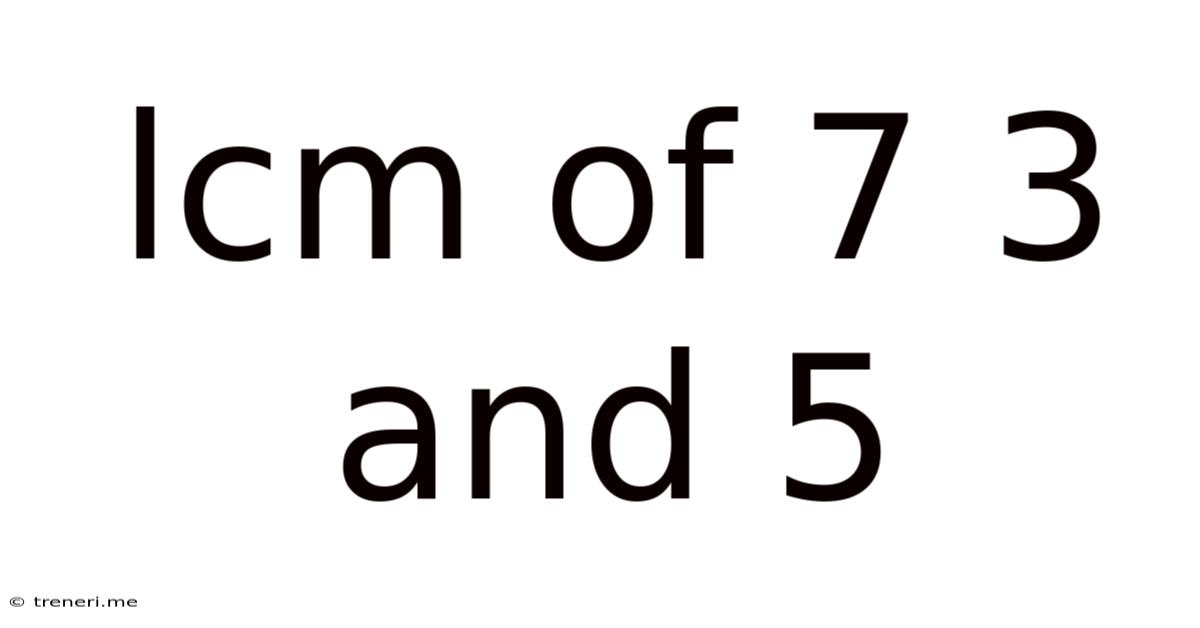
Table of Contents
Finding the LCM of 7, 3, and 5: A Comprehensive Guide
Finding the Least Common Multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to scheduling tasks. This comprehensive guide will delve into the methods of calculating the LCM of 7, 3, and 5, explore its real-world applications, and provide you with a strong understanding of this important mathematical operation.
Understanding Least Common Multiples (LCM)
Before diving into the calculation, let's solidify our understanding of LCM. The LCM of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... The multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Methods for Calculating the LCM of 7, 3, and 5
There are several methods to determine the LCM, each with its own advantages and disadvantages. Let's explore the most common ones, applying them to find the LCM of 7, 3, and 5.
1. Listing Multiples Method
This is a straightforward method, especially suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105...
By examining the lists, we can see that the smallest number that appears in all three lists is 105. Therefore, the LCM of 7, 3, and 5 is 105.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 5: 5 (5 is a prime number)
Since 7, 3, and 5 are all prime numbers and have no common factors, the LCM is simply the product of these three numbers: 7 * 3 * 5 = 105.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between LCM and GCD (Greatest Common Divisor). The formula connecting LCM and GCD for two numbers a and b is:
LCM(a, b) * GCD(a, b) = a * b
While this formula directly applies to two numbers, we can extend it to multiple numbers by finding the LCM iteratively. First, find the LCM of 7 and 3, then find the LCM of that result and 5.
- GCD(7, 3) = 1 (7 and 3 have no common factors other than 1)
- LCM(7, 3) = (7 * 3) / GCD(7, 3) = 21
- GCD(21, 5) = 1
- LCM(21, 5) = (21 * 5) / GCD(21, 5) = 105
Therefore, the LCM of 7, 3, and 5 is 105.
Real-World Applications of LCM
The concept of LCM has numerous practical applications in various fields:
1. Scheduling and Time Management
Imagine you have three different machines that operate on cycles: one every 7 days, another every 3 days, and the last one every 5 days. To determine when all three machines will be operational simultaneously, you need to find the LCM of 7, 3, and 5. The LCM, 105, indicates that all three machines will be operational together every 105 days. This is crucial for scheduling maintenance or coordinating tasks involving these machines.
2. Fraction Operations
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential for finding a common denominator. This allows for the simplification of fraction operations.
3. Music Theory
In music, the LCM is used to determine the least common period of two musical phrases with different lengths.
4. Gear Ratios
In mechanical engineering, gear ratios often involve finding the LCM to understand when gears will be in synchronization.
Beyond the Basics: Exploring LCM for Larger Numbers
While the methods described above work well for smaller numbers like 7, 3, and 5, dealing with larger numbers might require more advanced techniques or the use of computational tools. For example, the prime factorization method becomes more complex with larger numbers requiring more effort in finding their prime factors. In such cases, algorithms and software can significantly simplify the process.
Conclusion: Mastering the LCM
The LCM, a seemingly simple concept, holds significant importance across numerous mathematical and real-world applications. Understanding the various methods for calculating the LCM, as demonstrated with the example of 7, 3, and 5, empowers you to tackle more complex problems effectively. Whether using the listing method, prime factorization, or the GCD approach, choosing the appropriate method depends on the specific numbers involved and the tools at your disposal. Mastering the LCM opens doors to a deeper understanding of mathematical principles and enhances problem-solving capabilities in various practical scenarios. Remember to always choose the method that best suits your needs and the complexity of the numbers involved. The ultimate goal is to find the smallest positive integer divisible by all the numbers in question, efficiently and accurately. This understanding forms a strong foundation for more advanced mathematical concepts and practical applications.
Latest Posts
Latest Posts
-
10 Out Of 21 As A Percentage
May 12, 2025
-
How Much Omega 3 Per Day For Dogs
May 12, 2025
-
7 Out Of 10 As A Grade
May 12, 2025
-
60 Days From November 12 2024
May 12, 2025
-
How Much Bbq For 100 People
May 12, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 7 3 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.