10 Out Of 21 As A Percentage
Treneri
May 12, 2025 · 5 min read
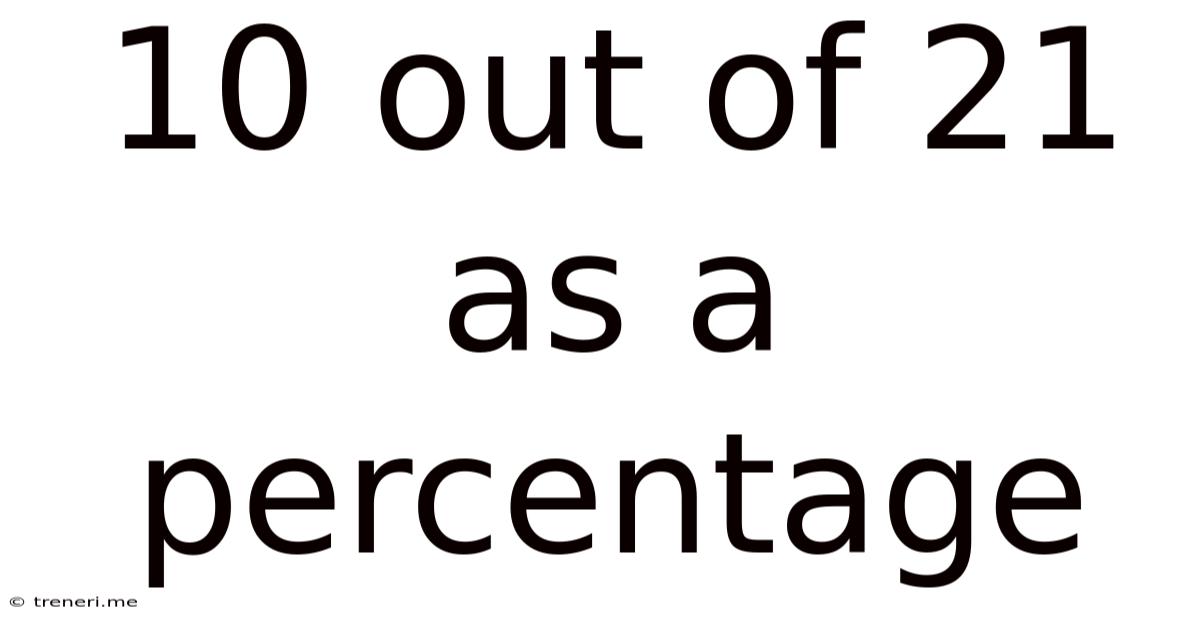
Table of Contents
10 Out of 21 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic assessments to financial transactions and everyday decision-making. Understanding how to convert fractions into percentages is crucial for interpreting data, making comparisons, and solving practical problems. This comprehensive guide will delve into the calculation of "10 out of 21 as a percentage," exploring different methods, providing step-by-step instructions, and offering practical examples to solidify your understanding. We'll also discuss the importance of percentage calculations and their relevance in various fields.
Understanding Percentages: The Basics
Before we tackle the specific calculation, let's establish a solid foundation in percentage concepts. A percentage is simply a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% signifies 50 out of 100, which is equivalent to one-half (½) or 0.5 in decimal form.
The fundamental formula for calculating a percentage is:
(Part / Whole) * 100% = Percentage
Where:
- Part: Represents the specific portion you're interested in.
- Whole: Represents the total amount or the entire quantity.
This formula is the cornerstone for converting any fraction into its percentage equivalent.
Calculating 10 Out of 21 as a Percentage: Step-by-Step
Now, let's apply this formula to determine "10 out of 21 as a percentage." In this scenario:
- Part = 10
- Whole = 21
Using the formula:
(10 / 21) * 100% = Percentage
-
Divide the part by the whole: 10 divided by 21 equals approximately 0.47619.
-
Multiply by 100: Multiply the result (0.47619) by 100 to express it as a percentage. This gives us approximately 47.619%.
-
Round to the desired precision: Depending on the context, you might round the percentage to a specific number of decimal places. Rounding to one decimal place, we get 47.6%. Rounding to the nearest whole number, we get 48%.
Therefore, 10 out of 21 is approximately 47.6% (or 48%, depending on the required level of accuracy).
Alternative Methods for Percentage Calculation
While the above method is straightforward, other approaches can be used to calculate percentages, particularly when dealing with more complex scenarios or when using different tools.
Using a Calculator:
Most calculators have a percentage function. Simply enter "10 ÷ 21 × 100" to obtain the percentage directly. This method provides a quick and accurate solution.
Using Spreadsheet Software:
Spreadsheet programs like Microsoft Excel or Google Sheets offer built-in functions for percentage calculations. The formula =(10/21)*100 in a cell will directly calculate and display the percentage. These programs also facilitate rounding and formatting for presentation purposes.
Using Online Percentage Calculators:
Numerous online percentage calculators are readily available. These tools provide a user-friendly interface for inputting values and obtaining the percentage result immediately. This option is particularly helpful for quick calculations without needing a calculator or spreadsheet software.
Practical Applications of Percentage Calculations
Percentage calculations are ubiquitous across various fields. Here are some examples:
Academic Performance:
Calculating grades, test scores, and overall academic performance often involves percentages. For example, if a student answers 10 out of 21 questions correctly on a test, their score would be approximately 47.6%.
Financial Matters:
Percentages are fundamental in finance, used to calculate interest rates, discounts, taxes, profits, losses, and investment returns. Understanding percentage changes in stock prices or understanding compound interest requires proficiency in percentage calculations.
Business and Economics:
Businesses utilize percentages for various purposes, including calculating profit margins, market share, growth rates, and sales figures. Economic indicators such as inflation rates, unemployment rates, and GDP growth are also expressed as percentages.
Statistics and Data Analysis:
Percentages are crucial for summarizing and interpreting data. Representing data using percentages makes it easier to compare and analyze different groups or categories. For example, in a survey, percentages are used to represent the proportion of respondents who chose a specific option.
Everyday Life:
Percentage calculations are used in everyday scenarios such as calculating tips in restaurants, determining discounts during sales, or understanding the nutritional content of food products. Being able to quickly calculate percentages makes everyday decisions easier and more informed.
Importance of Accuracy and Rounding
When calculating percentages, the level of accuracy is crucial. While rounding is often necessary for practical purposes, it's essential to be mindful of the potential impact on the overall result. In some situations, a precise percentage is required, whereas in others, an approximation might suffice. Always consider the context of the calculation to determine the appropriate level of rounding. Over-rounding can lead to significant errors, particularly when dealing with large sums of money or critical data.
Beyond the Basics: Percentage Change and Increase/Decrease
While this article focuses on calculating a simple percentage from a fraction, understanding percentage change is another crucial concept. This involves calculating the percentage difference between two values. The formula for percentage change is:
[(New Value - Old Value) / Old Value] * 100% = Percentage Change
This formula helps determine the percentage increase or decrease between two points in time or two different datasets. For instance, if a product's price increases from $10 to $12, the percentage increase is calculated as:
[(12 - 10) / 10] * 100% = 20%
Understanding percentage change is vital in various financial and economic analyses.
Conclusion: Mastering Percentage Calculations
The ability to calculate percentages accurately and efficiently is a valuable skill applicable to numerous aspects of life. Understanding the fundamental formula, various calculation methods, and the significance of accuracy and rounding will significantly enhance your problem-solving abilities. From everyday tasks to complex financial analyses, mastering percentage calculations provides a strong foundation for success in various fields. This comprehensive guide aims to equip you with the knowledge and skills necessary for confidently tackling any percentage calculation, regardless of its complexity. Remember that practice is key to solidifying your understanding and improving your speed and accuracy in these crucial calculations.
Latest Posts
Latest Posts
-
Cuanto Son 100 Grados Fahrenheit En Celsius
May 12, 2025
-
What Is 1 1 3 Minus 2 3
May 12, 2025
-
5 7 Divided By 1 3
May 12, 2025
-
Cuanto Es 50 Millones De Pesos
May 12, 2025
-
5 8 2 5 As A Fraction
May 12, 2025
Related Post
Thank you for visiting our website which covers about 10 Out Of 21 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.