Lcm Of 93 62 And 120
Treneri
May 14, 2025 · 5 min read
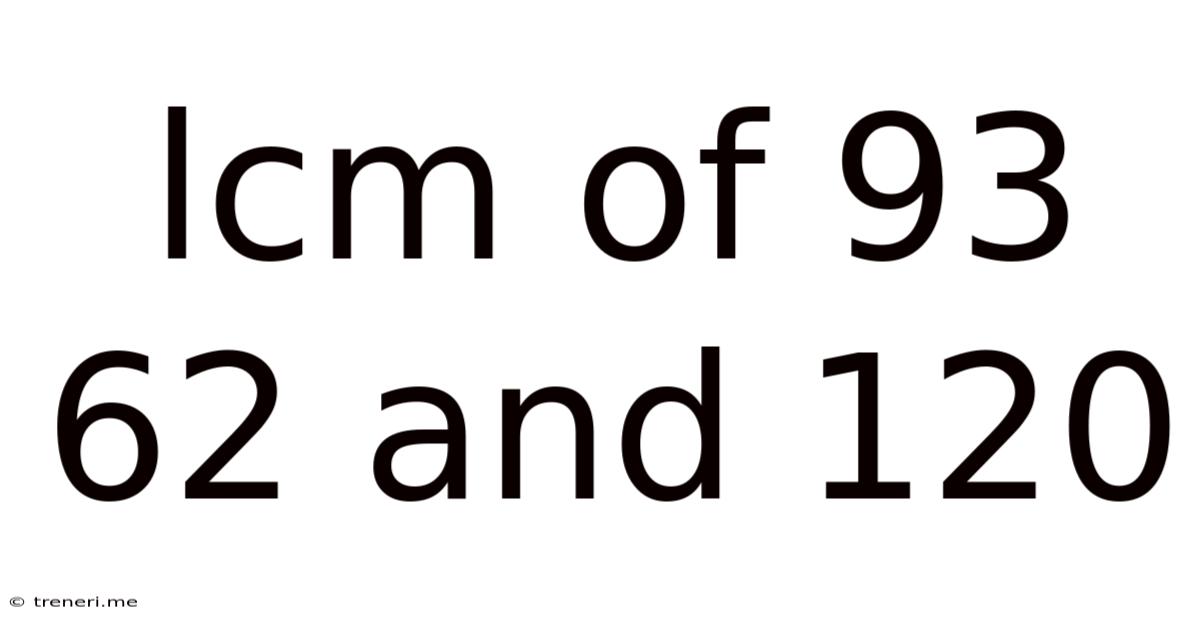
Table of Contents
Finding the Least Common Multiple (LCM) of 93, 62, and 120: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers might seem like a simple mathematical task, but understanding the underlying principles and employing efficient methods can significantly improve your problem-solving skills. This article delves deep into calculating the LCM of 93, 62, and 120, explaining various methods and their applications. We'll explore the concept of LCM, its significance in different fields, and provide a step-by-step approach to solve this specific problem, along with practical examples to solidify your understanding.
Understanding the Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. This concept is fundamental in various mathematical applications, including simplifying fractions, solving problems involving ratios and proportions, and scheduling cyclical events. Understanding LCM is crucial for anyone working with numbers, from students to professionals in fields like engineering and computer science.
Why is LCM Important?
The LCM isn't just a theoretical concept; it has practical real-world applications:
-
Scheduling: Imagine you have two machines that operate on cycles. One runs every 93 minutes, and the other every 62 minutes. The LCM helps you determine when both machines will be at their starting point simultaneously.
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators allows you to find a common denominator, simplifying the calculation.
-
Project Management: In project management, the LCM can help coordinate tasks with different completion times, ensuring optimal resource utilization and timely project completion.
-
Music: In music theory, the LCM is used to determine the least common denominator of musical rhythms and time signatures.
Methods for Calculating the LCM
Several methods exist for finding the LCM, each with its advantages and disadvantages. We'll explore the most common and efficient ones, focusing on their application to finding the LCM of 93, 62, and 120.
1. Prime Factorization Method
This method is considered one of the most fundamental and reliable ways to calculate the LCM. It involves breaking down each number into its prime factors. The prime factors are the prime numbers that when multiplied together, result in the original number.
Steps:
-
Find the prime factorization of each number:
- 93 = 3 x 31
- 62 = 2 x 31
- 120 = 2 x 2 x 2 x 3 x 5 = 2³ x 3 x 5
-
Identify the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, 5, and 31.
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
- The highest power of 31 is 31¹ = 31
-
Multiply the highest powers together:
LCM(93, 62, 120) = 2³ x 3 x 5 x 31 = 8 x 3 x 5 x 31 = 3720
Therefore, the least common multiple of 93, 62, and 120 is 3720.
2. Listing Multiples Method
This method is straightforward but can be time-consuming, especially with larger numbers. It involves listing multiples of each number until you find the smallest common multiple.
Steps:
-
List multiples of each number:
-
Multiples of 93: 93, 186, 279, 372, 465, 558, 651, 744, 837, 930, 1023, 1116, 1209, 1302, 1395, 1488, 1581, 1674, 1767, 1860, 1953, 2046, 2139, 2232, 2325, 2418, 2511, 2604, 2697, 2790, 2883, 2976, 3069, 3162, 3255, 3348, 3441, 3534, 3627, 3720...
-
Multiples of 62: 62, 124, 186, 248, 310, 372, 434, 496, 558, 620, 682, 744, 806, 868, 930, 992, 1054, 1116, 1178, 1240, 1302, 1364, 1426, 1488, 1550, 1612, 1674, 1736, 1798, 1860, 1922, 1984, 2046, 2108, 2170, 2232, 2294, 2356, 2418, 2480, 2542, 2604, 2666, 2728, 2790, 2852, 2914, 2976, 3038, 3100, 3162, 3224, 3286, 3348, 3410, 3472, 3534, 3596, 3658, 3720...
-
Multiples of 120: 120, 240, 360, 480, 600, 720, 840, 960, 1080, 1200, 1320, 1440, 1560, 1680, 1800, 1920, 2040, 2160, 2280, 2400, 2520, 2640, 2760, 2880, 3000, 3120, 3240, 3360, 3480, 3600, 3720...
-
-
Find the smallest common multiple: The smallest multiple common to all three lists is 3720.
Therefore, the LCM(93, 62, 120) = 3720.
3. Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. You can find the LCM using the GCD, which is often easier to compute for larger numbers. The relationship is:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
However, this formula directly applies only to two numbers. For multiple numbers, you need to apply it iteratively. For three numbers a, b, and c:
First find LCM(a,b) = (a*b)/GCD(a,b)
Then find LCM(LCM(a,b),c) = (LCM(a,b)*c)/GCD(LCM(a,b),c)
Let's use the Euclidean Algorithm to find the GCD:
-
Find GCD(93, 62):
- 93 = 1 x 62 + 31
- 62 = 2 x 31 + 0
GCD(93, 62) = 31
-
Find GCD(31, 120):
- 120 = 3 x 31 + 27
- 31 = 1 x 27 + 4
- 27 = 6 x 4 + 3
- 4 = 1 x 3 + 1
- 3 = 3 x 1 + 0
GCD(31, 120) = 1
Now we apply the formula iteratively:
LCM(93,62) = (93*62)/31 = 186
LCM(186,120) = (186*120)/GCD(186,120)
To find GCD(186,120):
186 = 1120 + 66 120 = 166 + 54 66 = 154 + 12 54 = 412 + 6 12 = 2*6 +0
GCD(186,120) = 6
LCM(186,120) = (186*120)/6 = 3720
Therefore, the LCM(93, 62, 120) = 3720.
Conclusion
Finding the LCM of 93, 62, and 120 can be accomplished using several methods. The prime factorization method offers a clear and efficient approach, especially for larger numbers. The listing multiples method is suitable for smaller numbers, while the GCD method provides an alternative approach leveraging the relationship between LCM and GCD. Understanding these methods and their applications empowers you to tackle similar problems effectively and appreciate the versatility of LCM in various mathematical and real-world contexts. Remember to choose the method that best suits your needs and the complexity of the numbers involved. The key is to understand the underlying concepts and apply them consistently to achieve accurate results. The versatility of the LCM makes it an essential tool in various applications beyond simple mathematical exercises.
Latest Posts
Latest Posts
-
85 Rounded To The Nearest Hundred
May 14, 2025
-
5 Out Of 15 Is What Percent
May 14, 2025
-
Half Ounce Equals How Many Grams
May 14, 2025
-
2 Cups Of Heavy Cream In Ml
May 14, 2025
-
What Is The Distance Between 5 And 2
May 14, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 93 62 And 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.