Least Common Multiple Of 4 6 7
Treneri
May 10, 2025 · 5 min read
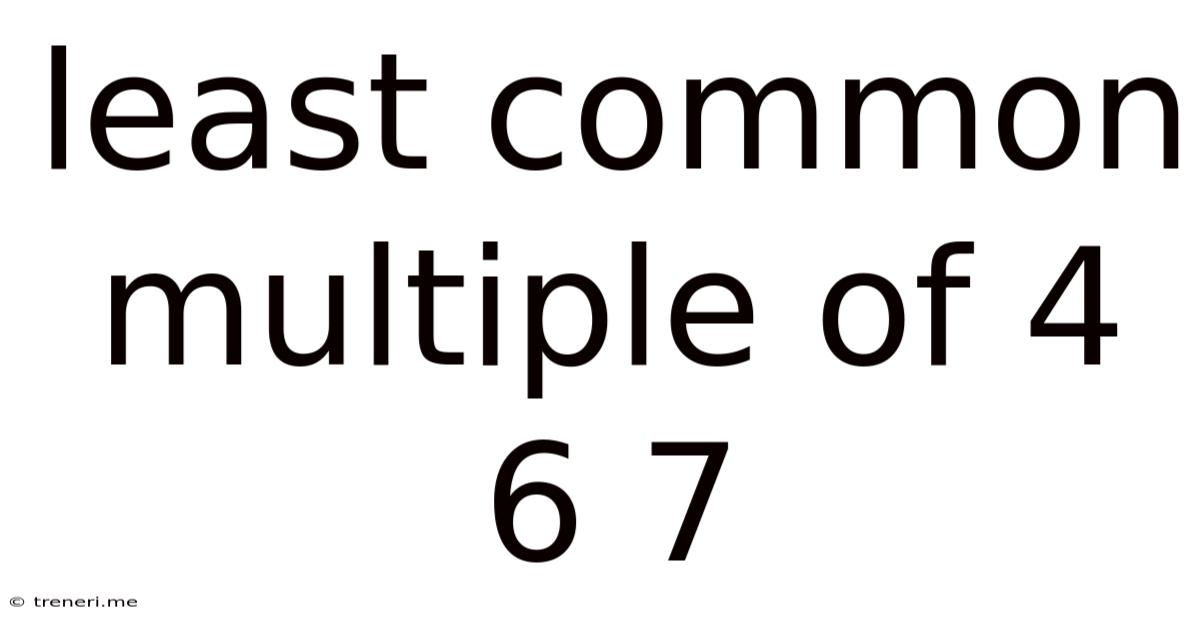
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 6, and 7: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and algebra. Understanding how to calculate the LCM is crucial for solving various problems involving fractions, ratios, and cyclical events. This article delves into the methods for finding the LCM of 4, 6, and 7, providing a detailed explanation and exploring different approaches. We'll also touch upon the broader applications of LCM and its significance in various mathematical contexts.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 4, 6, and 7, let's establish a clear understanding of what the LCM represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple is the smallest of these common multiples, which is 6.
Methods for Calculating LCM
Several methods exist for calculating the LCM of a set of numbers. We'll explore three primary methods, applying them to find the LCM of 4, 6, and 7:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, ...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, ...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, ...
By comparing the lists, we observe that the smallest common multiple of 4, 6, and 7 is 84.
Therefore, the LCM(4, 6, 7) = 84
This method becomes less efficient as the numbers involved increase in size.
2. Prime Factorization Method
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 4: 2²
- Prime factorization of 6: 2 × 3
- Prime factorization of 7: 7
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 7 is 7¹ = 7
Now, multiply these highest powers together: 4 × 3 × 7 = 84
Therefore, the LCM(4, 6, 7) = 84
This method is generally preferred for its efficiency and applicability to larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. While this method is less intuitive for more than two numbers, it can still be applied using a stepwise approach.
First, let's find the GCD of 4 and 6 using the Euclidean algorithm:
6 = 1 × 4 + 2 4 = 2 × 2 + 0
The GCD(4, 6) = 2
Now, we use the formula: LCM(a, b) = (a × b) / GCD(a, b)
LCM(4, 6) = (4 × 6) / 2 = 12
Next, we find the LCM of 12 and 7 using the same process. First, find the GCD(12, 7):
12 = 1 × 7 + 5 7 = 1 × 5 + 2 5 = 2 × 2 + 1 2 = 2 × 1 + 0
The GCD(12, 7) = 1
LCM(12, 7) = (12 × 7) / 1 = 84
Therefore, the LCM(4, 6, 7) = 84
Applications of LCM
The concept of LCM finds applications in various areas:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions involves calculating the LCM of the denominators.
-
Scheduling Problems: Determining when events will occur simultaneously (e.g., buses arriving at a stop, machines completing cycles) often requires finding the LCM of the cycle times.
-
Repeating Decimal Expansions: Understanding the length of the repeating part of a decimal expansion involves LCMs.
-
Modular Arithmetic: LCMs play a crucial role in solving problems related to congruences and modular arithmetic.
-
Music Theory: LCMs are used in music theory to determine the least common multiple of different note durations.
Conclusion: The LCM of 4, 6, and 7
Through three different methods – listing multiples, prime factorization, and the GCD method – we've consistently found that the least common multiple of 4, 6, and 7 is 84. Understanding the LCM and the various methods for calculating it is vital for various mathematical applications, extending beyond simple number theory to practical problem-solving across diverse fields. Choosing the most appropriate method depends on the complexity of the numbers involved, with prime factorization offering a more efficient approach for larger numbers. The importance of understanding LCMs can't be overstated; it's a fundamental building block for more advanced mathematical concepts. Mastering the calculation of the LCM provides a strong foundation for more advanced studies in mathematics and its applications.
Latest Posts
Latest Posts
-
What Percent Is 2 Out Of 11
May 10, 2025
-
What Is 35 8 As A Mixed Number
May 10, 2025
-
How Much Years Is 4960 Weeks
May 10, 2025
-
Cuanto Falta Para El 8 De Abril
May 10, 2025
-
1 5 1 5 1 5
May 10, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 4 6 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.