The Length Of The Arc Subtended By Θ Is S
Treneri
May 14, 2025 · 6 min read
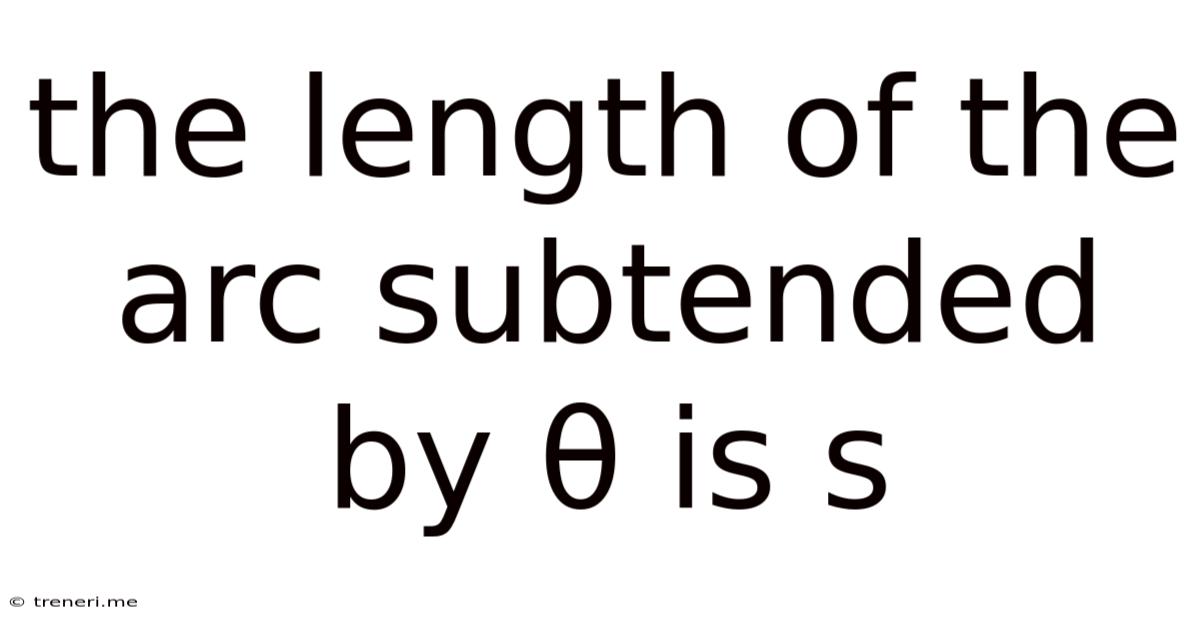
Table of Contents
The Length of the Arc Subtended by θ is s: A Deep Dive into Arc Length
The simple equation, s = rθ, elegantly encapsulates a fundamental concept in geometry and trigonometry: the relationship between arc length (s), radius (r), and the subtended angle (θ) in radians. This seemingly straightforward formula unlocks a wealth of applications in various fields, from engineering and physics to computer graphics and cartography. This article delves deep into the meaning, derivation, applications, and nuances of this crucial equation.
Understanding the Fundamentals: Radians, Angles, and Arcs
Before we dissect the equation s = rθ, let's solidify our understanding of the core components:
1. Radians: The Natural Unit of Angular Measurement
Radians are a crucial element in understanding arc length. Unlike degrees, which are arbitrary units based on dividing a circle into 360 parts, radians are defined by the ratio of the arc length to the radius. One radian is the angle subtended at the center of a circle by an arc whose length is equal to the radius. This inherent connection between arc length and radius makes radians the natural unit for measuring angles in many mathematical contexts.
Key takeaway: Radians directly relate angle measure to the length of the arc it subtends, making the formula s = rθ both elegant and intuitive.
2. The Subtended Angle (θ): The Heart of the Equation
The angle θ in the equation s = rθ is the central angle subtended by the arc. This means it's the angle formed at the center of the circle by the two radii that connect to the endpoints of the arc. It is crucial to remember that θ must be expressed in radians for the equation to be valid.
3. Arc Length (s): The Distance Along the Curve
The arc length (s) represents the distance along the curved path of the arc. It's not the straight-line distance between the endpoints of the arc (which would be a chord), but rather the length measured along the circumference of the circle.
Deriving the Equation: s = rθ
The derivation of s = rθ is elegantly simple and directly stems from the definition of a radian. Consider a circle with radius r. If we consider an arc with length equal to the radius (r), the angle subtended at the center is defined as 1 radian.
Now, let's generalize this. If we have an arc of length s, and the radius is still r, then the ratio of the arc length to the radius (s/r) represents the angle in radians. Therefore:
θ (in radians) = s/r
Rearranging this equation, we get the familiar form:
s = rθ
This simple derivation beautifully illustrates the direct proportionality between arc length, radius, and the subtended angle (in radians).
Applications of the Arc Length Formula: A Diverse Range of Uses
The equation s = rθ is not just a theoretical concept; it finds practical application in a multitude of fields. Here are some examples:
1. Engineering and Physics: Circular Motion and Rotational Mechanics
In engineering and physics, understanding arc length is fundamental for analyzing circular motion. Calculating the distance traveled by a point on a rotating object, determining the linear speed of a rotating component, or analyzing the path of a projectile moving in a circular arc all rely heavily on the formula. Consider, for example, the design of gears, wheels, or rotating machinery. Accurate calculation of arc lengths is crucial for optimal performance and efficiency.
2. Computer Graphics and Animation: Creating Smooth Curves and Paths
In the world of computer graphics and animation, the arc length formula plays a vital role in creating smooth curves and paths. Creating realistic animations of rotating objects or designing smooth transitions between different points requires precise control over the arc lengths involved. Techniques like Bezier curves and spline interpolation frequently use variations of this formula.
3. Cartography and Geography: Measuring Distances on Earth's Surface
Although the Earth is not perfectly spherical, the concept of arc length is still useful for approximating distances on its surface. By treating small portions of the Earth's surface as segments of a sphere, we can use the formula to estimate the distances between locations, particularly when dealing with shorter distances. Consider the problem of calculating the distance between two points along a latitude or longitude line.
4. Astronomy: Calculating Angular Sizes and Distances
In astronomy, the arc length formula helps astronomers calculate the angular sizes of celestial objects and estimate distances. By knowing the angular size of an object and its distance, we can infer its actual physical size. Conversely, knowing both the angular size and physical size, we can estimate the distance.
5. Mathematics: Calculus and Integration
The arc length formula forms a foundation for more advanced concepts in calculus, specifically in the calculation of arc length for more complex curves which are not simply segments of circles. The integral formula for arc length generalizes the simple equation we've been discussing to curves defined by functions.
Beyond the Basics: Exploring Complexities and Nuances
While the formula s = rθ provides a straightforward calculation for arc length, certain nuances require careful consideration:
1. Units: Radians are Essential
It is paramount to remember that the angle θ must be expressed in radians. Using degrees will lead to incorrect results. Always ensure your angle is converted to radians before applying the formula. Remember that 180 degrees is equivalent to π radians.
2. Sector Area: Extending the Concept
The arc length formula is closely related to the area of a sector of a circle. The area (A) of a sector is given by:
A = (1/2)r²θ
This demonstrates the interconnectedness of arc length, sector area, and the subtended angle.
3. Dealing with Large Angles: Complete Revolutions
The formula works seamlessly for angles greater than 2π radians (a complete revolution). The arc length will simply represent the length of multiple revolutions around the circle.
4. Applications in Three Dimensions: Spherical Geometry
While the formula directly applies to two-dimensional circles, the principles can be extended to three-dimensional spheres, leading to concepts like spherical coordinates and the calculation of distances on the surface of a sphere. This has significant implications in fields like GPS and satellite navigation.
Conclusion: The Enduring Importance of s = rθ
The equation s = rθ is a cornerstone of geometry and trigonometry. Its simplicity belies its power and versatility, finding application across a broad spectrum of disciplines. By understanding its derivation, applications, and subtleties, one gains a deeper appreciation for the fundamental relationship between arc length, radius, and the subtended angle. This formula serves not only as a tool for solving practical problems but also as a gateway to more advanced concepts in mathematics and related fields. Its importance continues to resonate across numerous scientific and technological advancements.
Latest Posts
Latest Posts
-
How Many Years Is 109 Months
May 14, 2025
-
What Is The Gcf Of 52 And 78
May 14, 2025
-
Is 8 10 Equivalent To 4 5
May 14, 2025
-
How Much More Time Until 12 Pm
May 14, 2025
-
1984 A 2024 Cuantos Anos Son
May 14, 2025
Related Post
Thank you for visiting our website which covers about The Length Of The Arc Subtended By Θ Is S . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.