What Are Two Equivalent Fractions For 10/12
Treneri
May 15, 2025 · 5 min read
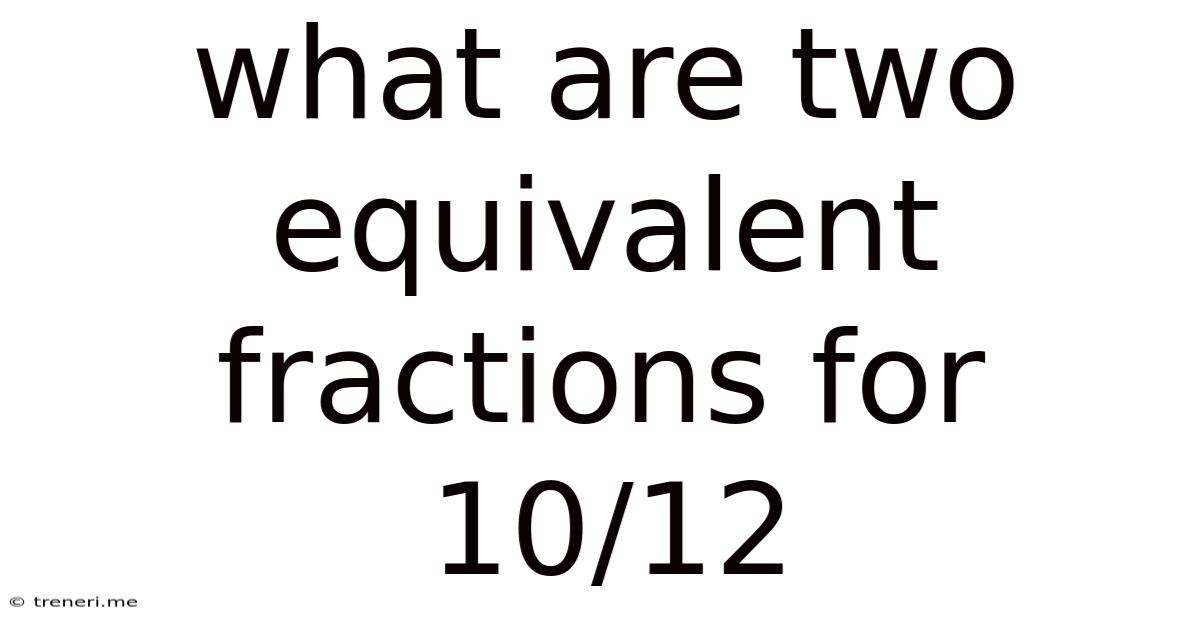
Table of Contents
What Are Two Equivalent Fractions for 10/12? A Deep Dive into Fraction Equivalence
Finding equivalent fractions is a fundamental concept in mathematics, crucial for understanding various aspects of arithmetic, algebra, and even real-world applications. This article will not only answer the question "What are two equivalent fractions for 10/12?" but will also delve deep into the underlying principles of fraction equivalence, providing you with a comprehensive understanding of the topic. We will explore various methods for finding equivalent fractions, demonstrate their practical applications, and offer examples to solidify your comprehension.
Understanding Fractions and Their Representation
Before we dive into finding equivalent fractions for 10/12, let's briefly revisit the concept of fractions. A fraction represents a part of a whole. It's written in the form a/b, where 'a' is the numerator (the part) and 'b' is the denominator (the whole). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
For example: In the fraction 10/12, the numerator (10) represents the number of parts we are interested in, and the denominator (12) represents the total number of equal parts the whole is divided into.
Equivalent Fractions: The Core Concept
Equivalent fractions are fractions that represent the same value, even though they look different. They are essentially different ways of expressing the same portion of a whole. Imagine slicing a pizza into 12 slices and taking 10. Now imagine slicing an identical pizza into 6 slices and taking 5. You've consumed the same amount of pizza in both instances, even though the fractions representing the consumed portion are different (10/12 and 5/6).
Finding Equivalent Fractions for 10/12: Methods and Examples
There are two primary methods to find equivalent fractions:
Method 1: Multiplying the Numerator and Denominator by the Same Number
The most straightforward method is to multiply both the numerator and the denominator of the fraction by the same non-zero number. This process does not change the value of the fraction because you're essentially multiplying by 1 (any number divided by itself equals 1).
Let's find two equivalent fractions for 10/12 using this method:
-
Multiply by 2: (10 x 2) / (12 x 2) = 20/24. Therefore, 20/24 is an equivalent fraction to 10/12.
-
Multiply by 3: (10 x 3) / (12 x 3) = 30/36. Therefore, 30/36 is another equivalent fraction to 10/12.
You can multiply by any non-zero number; you'll always obtain an equivalent fraction. This method generates infinitely many equivalent fractions.
Method 2: Dividing the Numerator and Denominator by Their Greatest Common Divisor (GCD)
This method is particularly useful for simplifying fractions to their lowest terms. The greatest common divisor (GCD) is the largest number that divides both the numerator and denominator without leaving a remainder. Dividing both by the GCD simplifies the fraction without changing its value.
To find equivalent fractions for 10/12 using this method, we first need to find the GCD of 10 and 12. The factors of 10 are 1, 2, 5, and 10. The factors of 12 are 1, 2, 3, 4, 6, and 12. The greatest common factor is 2.
- Divide by the GCD (2): (10 ÷ 2) / (12 ÷ 2) = 5/6. Therefore, 5/6 is an equivalent fraction to 10/12, and it's the simplest form of the fraction.
Why Finding Equivalent Fractions is Important
Understanding and utilizing equivalent fractions is essential in various mathematical contexts:
-
Simplifying Fractions: Reducing fractions to their simplest form improves readability and makes calculations easier.
-
Comparing Fractions: Finding equivalent fractions with a common denominator allows for easy comparison of fractions with different denominators.
-
Adding and Subtracting Fractions: Adding and subtracting fractions requires a common denominator, often achieved by finding equivalent fractions.
-
Solving Equations: Equivalent fractions are crucial in solving algebraic equations involving fractions.
-
Real-World Applications: Equivalent fractions find applications in various real-world scenarios, such as dividing resources, calculating proportions, and understanding ratios. For example, if you have a recipe that calls for 10 tablespoons of sugar out of a total of 12 tablespoons of ingredients, you can simplify this ratio to 5 tablespoons of sugar for every 6 tablespoons of ingredients (5/6).
Further Exploration: Infinite Equivalent Fractions
It's important to understand that for any given fraction, there are infinitely many equivalent fractions. You can generate as many as you need by repeatedly multiplying the numerator and denominator by the same non-zero number. This concept is closely related to the idea of proportionality and ratio.
Practical Examples: Applying Equivalent Fractions
Let's look at some real-world scenarios where understanding equivalent fractions is crucial:
Scenario 1: Baking a Cake: A recipe calls for 2/3 cup of flour. You only have a 1/4 cup measuring cup. To determine how many 1/4 cups of flour you need, you need to find an equivalent fraction of 2/3 with a denominator of 4. This involves finding a common denominator and converting the fractions.
Scenario 2: Sharing Pizza: Imagine you have a pizza cut into 12 slices, and you want to share it equally among 3 people. To figure out how many slices each person gets, you'd find an equivalent fraction of 12/12 (the whole pizza) with a denominator of 3.
Scenario 3: Building a Fence: If a fence requires 10 feet of wood out of a 12-foot length, you can simplify this ratio using equivalent fractions to understand the proportion of wood needed. This allows for accurate estimations and calculations during the construction process.
Conclusion: Mastering Equivalent Fractions
Finding equivalent fractions for 10/12, or any fraction for that matter, is a fundamental skill with wide-ranging applications. By understanding the principles of fraction equivalence and applying the methods outlined in this article – multiplying/dividing by the same number and using the GCD – you can confidently find equivalent fractions and apply this knowledge to various mathematical and real-world problems. Remember, the ability to manipulate and simplify fractions is a cornerstone of mathematical fluency. Practice is key to mastering this essential skill.
Latest Posts
Latest Posts
-
Is 2 A Factor Of 73
May 15, 2025
-
3 Oz Dry Pasta To Cooked
May 15, 2025
-
Greatest Common Factor Of 8 And 9
May 15, 2025
-
A Right Rectangular Prism Has A Height Of 9 Inches
May 15, 2025
-
A Desk Is How Many Meters High
May 15, 2025
Related Post
Thank you for visiting our website which covers about What Are Two Equivalent Fractions For 10/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.