What Is 1 2/5 As A Fraction
Treneri
May 13, 2025 · 5 min read
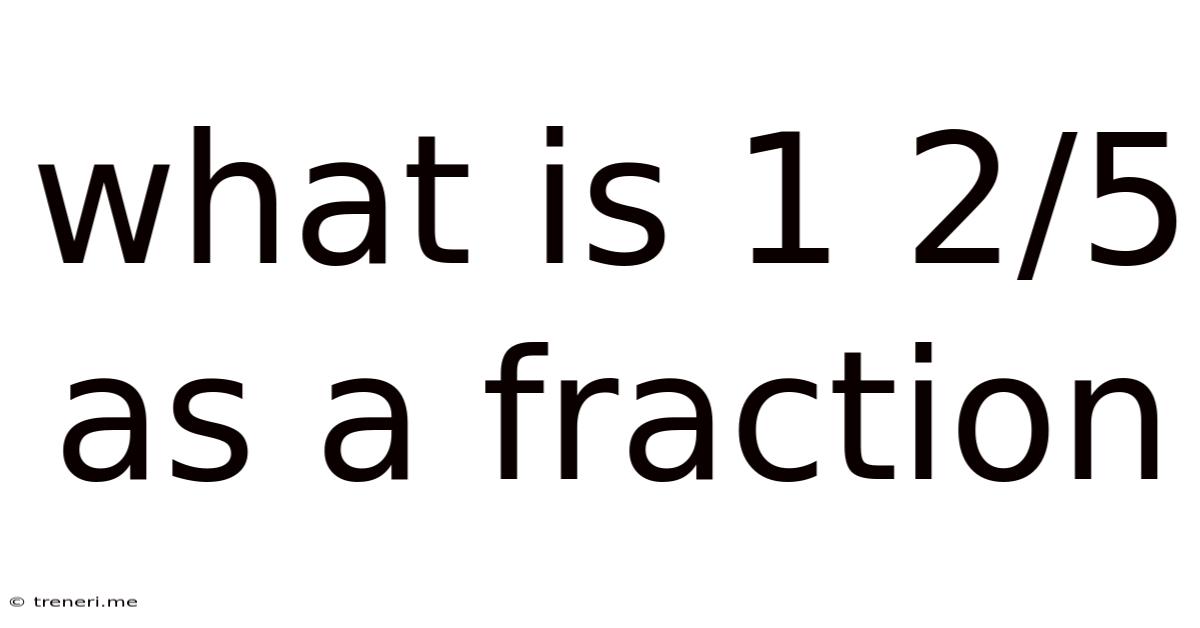
Table of Contents
What is 1 2/5 as a Fraction? A Comprehensive Guide
Understanding fractions is fundamental to mathematics, and converting mixed numbers like 1 2/5 into improper fractions is a crucial skill. This comprehensive guide will not only show you how to convert 1 2/5 into an improper fraction but also delve into the underlying concepts, providing you with a solid understanding of fractions and their manipulation. We'll cover various methods, explore practical applications, and even touch upon the history of fractions.
Understanding Mixed Numbers and Improper Fractions
Before we dive into the conversion, let's clarify the terminology:
-
Mixed Number: A mixed number combines a whole number and a fraction, such as 1 2/5. It represents a quantity greater than one.
-
Improper Fraction: An improper fraction has a numerator (the top number) that is greater than or equal to its denominator (the bottom number). For instance, 7/5 is an improper fraction.
Converting a mixed number to an improper fraction is a straightforward process, and mastering this skill is essential for various mathematical operations, including addition, subtraction, multiplication, and division of fractions.
Converting 1 2/5 to an Improper Fraction: Step-by-Step
The conversion of 1 2/5 to an improper fraction involves two simple steps:
Step 1: Multiply the whole number by the denominator.
In our case, the whole number is 1, and the denominator of the fraction 2/5 is 5. Therefore, we multiply 1 x 5 = 5.
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 2. Adding this to the result from Step 1 (5), we get 5 + 2 = 7.
Step 3: Keep the denominator the same.
The denominator remains unchanged. It stays as 5.
Therefore, 1 2/5 as an improper fraction is 7/5.
Visualizing the Conversion
Imagine you have one whole pizza and 2/5 of another pizza. To represent this as a single fraction, you need to express the entire amount in terms of fifths.
- One whole pizza can be divided into 5 slices (fifths). So, one whole pizza is 5/5.
- Adding the 2/5 from the second pizza, we get 5/5 + 2/5 = 7/5.
This visualization reinforces the concept of converting a mixed number to an improper fraction.
Alternative Methods for Conversion
While the above method is the most common and straightforward, there are other ways to approach the conversion:
-
Using a Diagram: Drawing a diagram representing the whole number and the fraction can provide a visual aid for understanding the process.
-
Using the Formula: The process can be summarized by the formula: Whole number + Numerator/Denominator = [(Whole number * Denominator) + Numerator] / Denominator
This formula directly applies the steps we've outlined above.
Practical Applications of Improper Fractions
Improper fractions are essential in various mathematical applications and real-world scenarios:
-
Baking: Recipes often require fractional amounts of ingredients. Converting mixed numbers to improper fractions simplifies calculations when combining ingredients.
-
Construction: Precise measurements are critical in construction. Improper fractions facilitate accurate calculations of lengths, volumes, and areas.
-
Advanced Mathematics: Algebra, calculus, and other advanced math topics rely heavily on fraction manipulation, where converting between mixed numbers and improper fractions is a fundamental step.
-
Data Analysis: Representing data using fractions often involves converting between mixed numbers and improper fractions for easier calculations and comparisons.
-
Financial Calculations: Working with percentages and proportions frequently necessitates converting mixed numbers to improper fractions to simplify calculations.
Common Mistakes to Avoid
When converting mixed numbers to improper fractions, be mindful of these common pitfalls:
-
Forgetting to add the numerator: Remember that the numerator must be added to the product of the whole number and the denominator.
-
Changing the denominator: The denominator remains unchanged throughout the conversion process.
-
Incorrect multiplication: Ensure accurate multiplication of the whole number and the denominator. A simple calculation error can lead to an incorrect improper fraction.
-
Not simplifying the fraction: After conversion, always check if the improper fraction can be simplified (reduced) to its lowest terms. For example, 10/10 can be simplified to 1.
Expanding Your Knowledge: Further Exploration of Fractions
Beyond the conversion of 1 2/5, understanding fractions in their entirety is crucial. Here are some areas to explore:
-
Adding and Subtracting Fractions: Learn how to add and subtract fractions with different denominators using techniques like finding the least common denominator (LCD).
-
Multiplying and Dividing Fractions: Master the rules of multiplying and dividing fractions, including simplifying the results.
-
Comparing Fractions: Develop the ability to compare and order fractions using techniques like finding common denominators or cross-multiplication.
-
Fractions and Decimals: Understand the relationship between fractions and decimals and learn how to convert between the two forms.
-
Fractions and Percentages: Explore the connections between fractions, decimals, and percentages and practice converting between these forms.
The History of Fractions: A Brief Overview
The concept of fractions has a rich history, dating back to ancient civilizations. Evidence suggests that the Egyptians used fractions as early as 1650 BC, primarily focusing on unit fractions (fractions with a numerator of 1). Babylonian mathematicians also worked with fractions, using a sexagesimal (base-60) system, which continues to influence our modern understanding of time and angles. The modern notation of fractions, with a numerator above a denominator and a line separating them, evolved over centuries, with contributions from various cultures and mathematicians.
Conclusion: Mastering Fraction Conversions
Converting 1 2/5 to the improper fraction 7/5 is a fundamental step in mastering fractions. Understanding the underlying concepts, practicing different methods, and avoiding common mistakes will equip you with the confidence to tackle more complex fractional calculations. By expanding your knowledge of fractions and their applications, you'll enhance your mathematical skills and open doors to a wider range of academic and practical applications. Remember to practice regularly, and you will soon find fraction manipulation to be second nature.
Latest Posts
Latest Posts
-
How To Make A Huge Circle In Minecraft
May 13, 2025
-
800 Grams Cottage Cheese To Cups
May 13, 2025
-
Cuanto Es 2 Litros De Agua En Onzas
May 13, 2025
-
30 Days After October 31 2024
May 13, 2025
-
1000 Board Feet To Square Feet
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 2/5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.