What Is 1 Percent Of 15
Treneri
May 09, 2025 · 4 min read
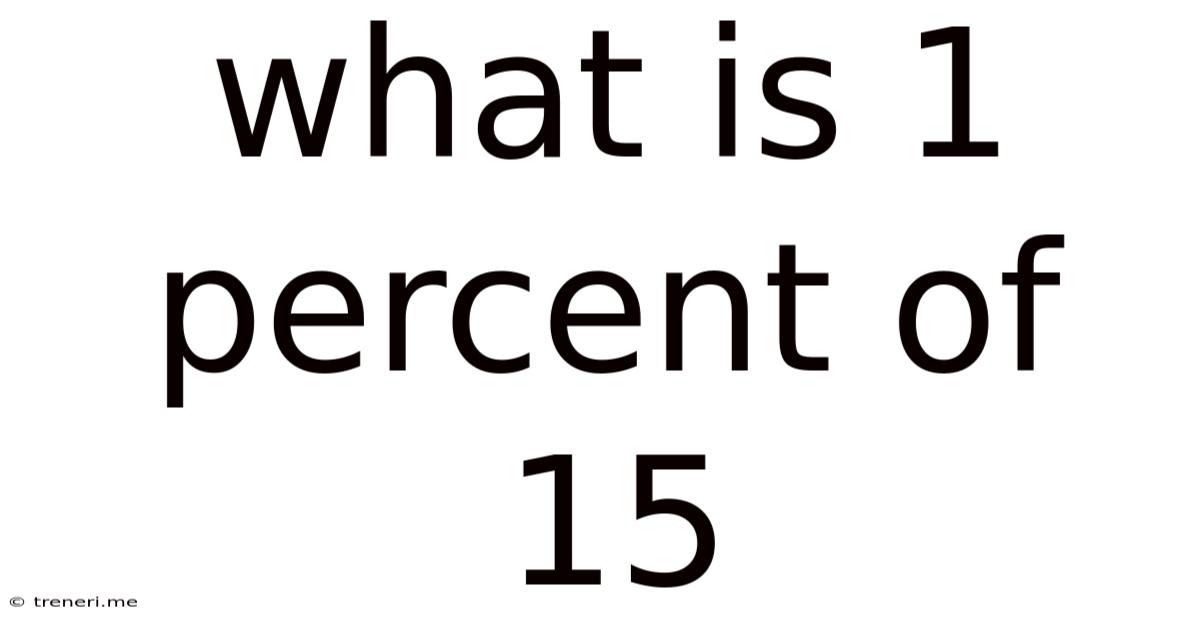
Table of Contents
What is 1 Percent of 15? A Deep Dive into Percentages and Their Applications
This seemingly simple question, "What is 1 percent of 15?", opens the door to a fascinating exploration of percentages, their practical applications, and the underlying mathematical concepts. While the answer itself is straightforward, understanding the how and why behind the calculation is crucial for various aspects of life, from everyday budgeting to complex financial modeling. This comprehensive guide will not only answer the question but also delve into the broader context of percentage calculations, offering practical examples and real-world applications.
Understanding Percentages: The Basics
Before we tackle the specific problem, let's establish a firm understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 1% means 1 out of 100, or 1/100. This fundamental understanding is the key to solving any percentage problem.
Converting Percentages to Decimals and Fractions
To perform calculations efficiently, it's often helpful to convert percentages into their decimal or fractional equivalents. To convert a percentage to a decimal, divide the percentage by 100. For example:
- 1% = 1/100 = 0.01
- 10% = 10/100 = 0.1
- 50% = 50/100 = 0.5
- 100% = 100/100 = 1
Converting a percentage to a fraction involves writing the percentage as the numerator and 100 as the denominator, then simplifying the fraction if possible. For example:
- 25% = 25/100 = 1/4
- 75% = 75/100 = 3/4
These conversions are invaluable for simplifying calculations and understanding the relationship between percentages, decimals, and fractions.
Calculating 1 Percent of 15
Now, let's address the core question: What is 1 percent of 15? We can solve this using several methods:
Method 1: Using the Decimal Equivalent
As we established, 1% is equivalent to 0.01. To find 1% of 15, we simply multiply 15 by 0.01:
15 * 0.01 = 0.15
Therefore, 1 percent of 15 is 0.15.
Method 2: Using the Fraction Equivalent
1% can also be expressed as the fraction 1/100. To find 1% of 15, we multiply 15 by 1/100:
15 * (1/100) = 15/100 = 0.15
Again, we arrive at the answer: 0.15.
Method 3: Using Proportions
A proportion is a statement that two ratios are equal. We can set up a proportion to solve for 1% of 15:
x/15 = 1/100
Cross-multiplying, we get:
100x = 15
Dividing both sides by 100:
x = 15/100 = 0.15
This method reinforces the concept of percentages as ratios and provides a different perspective on the calculation.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in many real-world scenarios:
Finance and Budgeting
- Interest Rates: Interest on loans, savings accounts, and credit cards is calculated as a percentage of the principal amount.
- Discounts and Sales: Retail stores frequently offer discounts expressed as percentages. Calculating the discounted price requires understanding percentage calculations.
- Taxes: Sales tax, income tax, and other taxes are calculated as a percentage of the taxable amount.
- Investment Returns: Investment returns are often expressed as percentages, representing the growth or decline in the value of an investment.
- Profit Margins: Businesses use percentage calculations to determine profit margins, which represent the percentage of revenue remaining after deducting costs.
Science and Statistics
- Data Analysis: Percentages are frequently used to represent proportions and trends in data analysis. For example, expressing the percentage of respondents who answered a survey question in a specific way.
- Probability and Statistics: Percentages are used extensively to express probabilities and likelihoods in various statistical contexts.
- Scientific Measurements: In various scientific fields, measurements and results are often expressed as percentages to indicate the extent or magnitude of a particular phenomenon.
Everyday Life
- Tip Calculations: Calculating a tip in a restaurant typically involves determining a percentage of the bill.
- Recipe Adjustments: Scaling up or down a recipe often requires adjusting ingredient amounts using percentage calculations.
- Comparing Prices: Determining which product offers a better value often requires comparing prices and discounts expressed as percentages.
Beyond the Basics: More Complex Percentage Problems
While calculating 1% of 15 is a simple example, percentage calculations can become significantly more complex. For example:
- Calculating percentage increase or decrease: This involves determining the percentage change between two values.
- Finding the original value after a percentage increase or decrease: This requires working backwards from the final value and the percentage change.
- Calculating compound interest: This involves calculating interest on the principal amount plus accumulated interest.
Mastering the fundamental principles of percentage calculations, as illustrated by the simple example of finding 1% of 15, provides a solid foundation for tackling more complex problems in various fields.
Conclusion: The Power of Understanding Percentages
The question "What is 1 percent of 15?" may seem trivial at first glance. However, by exploring the underlying mathematical concepts and practical applications, we reveal the significant role percentages play in our daily lives and across numerous disciplines. Understanding percentages is not just about memorizing formulas; it's about developing a conceptual grasp of ratios, proportions, and their real-world implications. This understanding empowers us to make informed decisions, analyze data effectively, and navigate the complexities of finance, science, and everyday life with confidence. The seemingly simple calculation of 0.15 represents the gateway to a world of practical application and deeper mathematical understanding.
Latest Posts
Latest Posts
-
Cuanto Son 28 Fahrenheit En Centigrados
May 09, 2025
-
How Many Seconds Is 10 Mins
May 09, 2025
-
What Is The Gcf Of 8 And 14
May 09, 2025
-
Cuanto Es 3 Pies En Metros
May 09, 2025
-
How Many Mm In 8 Cm
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 Percent Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.